AE 15: How much food do you get when you order Chipotle?

Inspired by this Reddit post, we will explore the differences in the weight of Chipotle orders. The data was originally collected by Zackary Smigel, and a cleaned copy be found in data/chipotle.csv.

Throughout the application exercise we will use the {infer} package which is part of {tidymodels} to estimate our bootstrap confidence intervals (CIs).

library(tidyverse)
library(tidymodels)
library(skimr)
library(gt) # for tables

chipotle <- read_csv(file = "data/chipotle.csv")

skim(chipotle)

Data summary

Name	chipotle
Number of rows	30
Number of columns	7
_______________________
Column type frequency:
character	4
Date	1
numeric	2
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	empty	n_unique	whitespace
order	0	1	6	6	0	2	0
meat	0	1	7	8	0	2	0
store	0	1	7	7	0	3	0
food	0	1	4	7	0	2	0

Variable type: Date

skim_variable	n_missing	complete_rate	min	max	median	n_unique
date	0	1	2024-01-12	2024-02-10	2024-01-26	30

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
day	0	1	15.5	8.80	1.00	8.25	15.50	22.75	30.00	▇▇▇▇▇
weight	0	1	810.8	123.37	510.29	715.82	793.79	907.18	1048.93	▁▆▇▇▂

The variable we will use in this analysis is weight which records the total weight of the order (in grams).

Typical weight of a Chipotle order

Observed sample

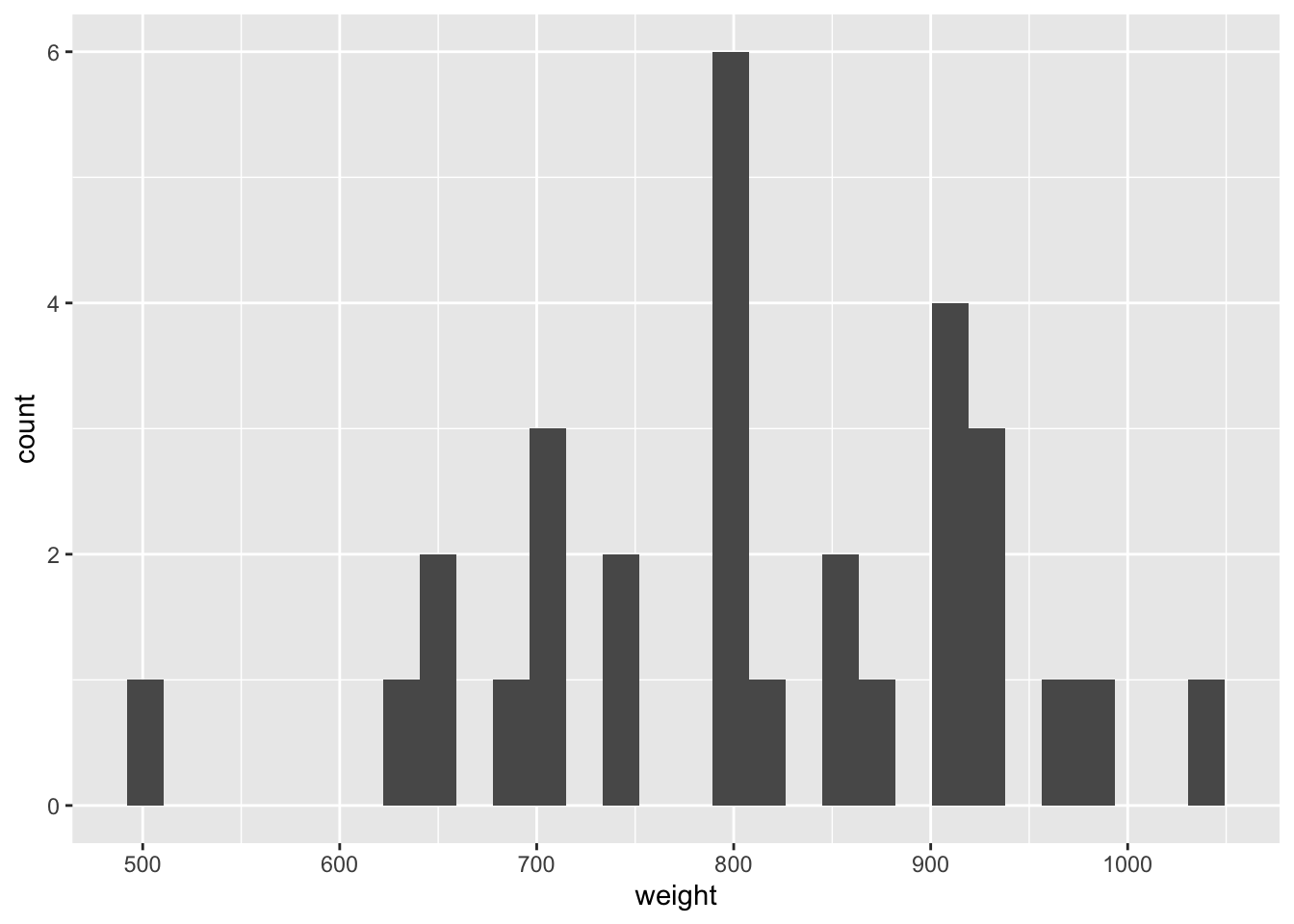
Demo: Visualize the distribution of weight using a histogram and calculate the arithmetic mean.

ggplot(data = chipotle, mapping = aes(x = weight)) +
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

chipotle |>
  summarize(mean = mean(weight))

# A tibble: 1 × 1
   mean
  <dbl>
1  811.

Your turn:

• What is the sample statistic?
• How large will each bootstrap sample be?
• How many bootstrap resamples do we need?

Generate bootstrap means

Demo: Calculate bootstrap means of the order weight. Create as many resamples as you determined above.

set.seed(123) # to ensure reproducibility

# observed difference
d_hat <- chipotle |>
  specify(response = weight) |>
  calculate(stat = "mean")

boot_df <- chipotle |>
  specify(response = weight) |>
  generate(reps = TODO, type = "bootstrap") |>
  calculate(stat = "mean")

Error: object 'TODO' not found

Your turn: Take a glimpse() of boot_df. What do you see?

glimpse(boot_df)

Error: object 'boot_df' not found

Your turn: Plot a histogram of boot_df. Where is it centered? Why does this make sense?

visualize(data = boot_df)

Error: object 'boot_df' not found

Create a 95% confidence interval

Demo: Now let’s use boot_df to create our 95% confidence interval.

get_ci(x = boot_df, level = 0.95)

Error: object 'boot_df' not found

Demo: Let’s visualize our confidence interval by adding a vertical line at each of these values.

visualize(data = boot_df) +
  shade_ci(endpoints = get_ci(x = boot_df, level = 0.95))

Error: object 'boot_df' not found

Interpreting confidence intervals

How do we interpret this confidence interval?

1. There is a 95% probability the true weight of Chipotle orders is between 766 and 854 grams.
2. There is a 95% probability the weight of Chipotle orders is between 766 and 854 grams.
3. We are 95% confident the true weight of Chipotle orders is between 766 and 854 grams.
4. We are 95% confident the weight of Chipotle orders is between 766 and 854 grams.

Add response here.

Alternative confidence intervals

Your turn: Create a 90% confidence interval. Report it below and visualize it with the histogram created above. Is it wider or more narrow than the 95% confidence interval?

# add code here

Add response here.

Difference in weight of Chipotle orders

We can calculate bootstrap confidence intervals for a range of statistical parameters.

Your turn: Estimate a 95% confidence interval for the difference in means between orders placed by a person and those placed online.

# observed difference
d_hat <- chipotle |>
  specify(TODO) |>
  calculate(stat = TODO, order = c("Person", "Online"))

# bootstrap CI
boot_diff_df <- chipotle |>
  TODO

visualize(boot_diff_df) +
  shade_confidence_interval(endpoints = get_ci(x = boot_diff_df, level = 0.95))

get_ci(x = boot_diff_df, level = 0.95)

Error in TODO: The pipe operator requires a function call as RHS (<input>:8:3)

How does that compare to the \(p\)-value from our hypothesis test?

null_dist <- chipotle |>
  # specify the response and explanatory variable
  specify(weight ~ order) |>
  # declare the null hypothesis
  hypothesize(null = "independence") |>
  # simulate the null distribution
  generate(reps = TODO, type = "permute") |>
  # calculate the difference in means for each permutation
  calculate(stat = "diff in means", order = c("Person", "Online"))

Error: object 'TODO' not found

# visualize simulated p-value
visualize(null_dist) +
  shade_p_value(obs_stat = d_hat, direction = "two-sided")

Error: object 'null_dist' not found

# calculate simulated p-value
null_dist |>
  get_p_value(obs_stat = d_hat, direction = "two-sided")

Error: object 'null_dist' not found

Add response here.

Multiple explanatory variables

We often calculate confidence intervals for the coefficients of multiple explanatory variables in a regression model. These can be useful in communicating our best guess as to the true value of the coefficient, and are often communicated as part of the results of a regression analysis.

Demo: Estimate the 95% confidence interval for the coefficients in the multiple variable model, and communicate them in a table and a coefficient plot.

# observed results
obs_fit <- chipotle |>
  specify(weight ~ order + meat + food + store) |>
  fit()

# null distribution for p-values
null_full_dist <- chipotle |>
  specify(weight ~ order + meat + food + store) |>
  hypothesize(null = "independence") |>
  generate(reps = TODO, type = "permute") |>
  fit()

Error: object 'TODO' not found

p_vals <- get_p_value(null_full_dist, obs_stat = obs_fit, direction = "two-sided")

Error: object 'null_full_dist' not found

# bootstrap distribution for CIs
boot_full_dist <- chipotle |>
  specify(weight ~ order + meat + food + store) |>
  generate(reps = TODO, type = "bootstrap") |>
  fit()

Error: object 'TODO' not found

# get 95% confidence interval
conf_ints <- get_ci(boot_full_dist, level = 0.95, point_estimate = obs_fit)

Error: object 'boot_full_dist' not found

# visualize regression results using a results table
obs_fit |>
  # join with p-values
  left_join(p_vals) |>
  # join with confidence intervals
  left_join(conf_ints) |>
  # print an HTML table
  gt() |>
  # format for 2 significant digits
  fmt_number(
    columns = c(estimate, p_value, lower_ci, upper_ci),
    decimals = 2
  )

Error: object 'p_vals' not found

# visualize regression results using a coefficient plot
obs_fit |>
  # join with confidence intervals
  left_join(conf_ints) |>
  # order the coefficients by size, pull intercept to the beginning (by convention)
  mutate(term = fct_reorder(.f = term, .x = estimate) |>
           fct_relevel("intercept")) |>
  # draw a pointrange plot
  ggplot(mapping = aes(x = estimate, y = term, xmin = lower_ci, xmax = upper_ci)) +
  geom_pointrange() +
  # draw a vertical line at 0
  geom_vline(xintercept = 0, linetype = "dashed") +
  theme_minimal()

Error: object 'conf_ints' not found