AE 16: Traffic fines and electoral politics - regression with a single predictor
Suggested answers
In this application exercise we will replicate part of the analysis from Playing politics with traffic fines: Sheriff elections and political cycles in traffic fines revenue.1 The abstract of the article states:
1 Su, Min, and Christian Buerger. 2025. “Playing politics with traffic fines: Sheriff elections and political cycles in traffic fines revenue.” American Journal of Political Science 69: 164–175. https://doi.org/10.1111/ajps.12866
The political budget cycle theory has extensively documented how politicians manipulate policies during election years to gain an electoral advantage. This paper focuses on county sheriffs, crucial but often neglected local officials, and investigates their opportunistic political behavior during elections. Using a panel data set covering 57 California county governments over four election cycles, we find compelling evidence of traffic enforcement policy manipulation by county sheriffs during election years. Specifically, a county’s per capita traffic fines revenue is 9% lower in the election than in nonelection years. The magnitude of the political cycle intensifies when an election is competitive. Our findings contribute to the political budget cycle theory and provide timely insights into the ongoing debate surrounding law enforcement reform and local governments’ increasing reliance on fines and fees revenue.
We will use {tidyverse} and {tidymodels} for data exploration and modeling, respectively.
The replication data file can be found in data/traffic_fines.csv. Let’s load the data and take a look at the first few rows.2
2 The codebook is available from Dataverse. The data set has been lightly cleaned for the application exercise.
traffic_fines <- read_csv("data/traffic_fines.csv")Rows: 1025 Columns: 38
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): county_name, elec_dummy
dbl (36): year, county_code, vehicle_code_fines, vehicle_code_fines_i_p, she...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.glimpse(traffic_fines)Rows: 1,025
Columns: 38
$ year <dbl> 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010,…
$ county_code <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ county_name <chr> "Alameda", "Alameda", "Alameda", "Alameda", "Al…
$ vehicle_code_fines <dbl> 4973766, 5701454, 4645572, 5256212, 5498544, 61…
$ vehicle_code_fines_i_p <dbl> 3.390001297, 3.789429426, 2.998037100, 3.274991…
$ elec_dummy <chr> "No", "No", "No", "Yes", "No", "No", "No", "Yes…
$ sheriff_incumb <dbl> NA, NA, NA, 0, NA, NA, NA, 1, NA, NA, NA, 1, NA…
$ pre_elec <dbl> 3, 2, 1, 0, 3, 2, 1, 0, 3, 2, 1, 0, 3, 2, 1, 0,…
$ no_incumb <dbl> 0, 0, 0, 1, 0, 0, 0, NA, 0, 0, 0, NA, 0, 0, 0, …
$ incumb <dbl> 0, 0, 0, NA, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1…
$ sheriff_margin <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ rep_share <dbl> 24.12914, 23.34603, 23.34603, 23.34603, 23.3460…
$ dem_share <dbl> 69.36355, 75.36176, 75.36176, 75.36176, 75.3617…
$ otherparty_share <dbl> 6.507315, 1.292216, 1.292216, 1.292216, 1.29221…
$ white_share <dbl> 38.81055, 38.18618, 37.55138, 36.97749, 36.3921…
$ asian_share <dbl> 22.9700470, 23.4097118, 23.8579330, 24.2536736,…
$ black_share <dbl> 13.79221725, 13.57556534, 13.35229397, 13.18081…
$ hispanic_share <dbl> 20.249336, 20.555365, 20.875692, 21.132017, 21.…
$ other_share <dbl> 4.177846, 4.273178, 4.362700, 4.455998, 4.54087…
$ young_drivers <dbl> 13.747941, 13.883005, 14.037847, 14.106328, 14.…
$ density <dbl> 1778.408447, 1776.412109, 1769.553955, 1775.562…
$ areain_square_miles <dbl> 825, 825, 825, 825, 825, 825, 825, 825, 825, 82…
$ med_inc <dbl> 56225, 57659, 60937, 64285, 68263, 70217, 68258…
$ unemp <dbl> 6.9, 5.9, 5.1, 4.4, 4.7, 6.2, 10.3, 10.9, 10.1,…
$ own_source_share <dbl> 41.07184, 36.20716, 41.50222, 42.68028, 45.6660…
$ emp_goods <dbl> 117444, 119457, 119701, 120023, 117638, 113131,…
$ emp_service <dbl> 450019, 440813, 445607, 453242, 459652, 466141,…
$ pay_goods_i <dbl> 58498.00, 59739.12, 57935.97, 59750.71, 59243.0…
$ pay_service_i <dbl> 44602.00, 45911.36, 46548.32, 47463.97, 48513.6…
$ arte_share <dbl> 1.5740343, 1.6364014, 1.6177933, 1.6885616, 1.6…
$ collect_share <dbl> 2.1427305, 2.1672187, 2.1728802, 2.1599128, 2.1…
$ cnty_le_sworn_1000p <dbl> 2.063813, 1.977428, 2.022766, 1.987249, 2.01029…
$ felony_tot_1000p <dbl> 14.047289, 13.687105, 13.538766, 12.706516, 13.…
$ misdemeanor_tot_1000p <dbl> 29.27370, 28.31380, 25.42603, 24.42999, 25.4998…
$ forfeitures_i_p <dbl> 6.1655664, 3.4768946, 6.1081676, 1.0144602, 1.3…
$ other_court_fines_i_p <dbl> 1.55856478, 0.08475058, 2.31785750, 1.49219465,…
$ delinquent_fines_i_p <dbl> 1.4636116, 0.7356105, 0.7866636, 0.8906603, 0.8…
$ vic_margin <dbl> NA, NA, NA, 0, NA, NA, NA, 0, NA, NA, NA, 0, NA…skim(traffic_fines)| Name | traffic_fines |
| Number of rows | 1025 |
| Number of columns | 38 |
| _______________________ | |
| Column type frequency: | |
| character | 2 |
| numeric | 36 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| county_name | 0 | 1 | 4 | 15 | 0 | 57 | 0 |
| elec_dummy | 0 | 1 | 2 | 3 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1.00 | 2011.49 | 5.19 | 2003.00 | 2007.00 | 2011.00 | 2016.00 | 2020.00 | ▇▆▇▆▇ |
| county_code | 0 | 1.00 | 29.37 | 16.86 | 1.00 | 15.00 | 29.00 | 44.00 | 58.00 | ▇▇▇▇▇ |
| vehicle_code_fines | 0 | 1.00 | 1640704.86 | 3145153.92 | 0.00 | 68944.00 | 429544.00 | 1545628.00 | 21712704.00 | ▇▁▁▁▁ |
| vehicle_code_fines_i_p | 0 | 1.00 | 3.90 | 7.23 | 0.00 | 0.43 | 2.16 | 4.87 | 108.73 | ▇▁▁▁▁ |
| sheriff_incumb | 807 | 0.21 | 0.75 | 0.44 | 0.00 | 0.25 | 1.00 | 1.00 | 1.00 | ▃▁▁▁▇ |
| pre_elec | 0 | 1.00 | 1.61 | 1.11 | 0.00 | 1.00 | 2.00 | 3.00 | 3.00 | ▆▆▁▇▇ |
| no_incumb | 163 | 0.84 | 0.06 | 0.24 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ▇▁▁▁▁ |
| incumb | 55 | 0.95 | 0.17 | 0.37 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ▇▁▁▁▂ |
| sheriff_margin | 918 | 0.10 | 0.24 | 0.17 | 0.00 | 0.10 | 0.23 | 0.32 | 0.97 | ▇▇▂▁▁ |
| rep_share | 0 | 1.00 | 46.75 | 13.67 | 14.66 | 36.42 | 48.13 | 57.27 | 74.83 | ▂▅▅▇▂ |
| dem_share | 0 | 1.00 | 49.60 | 13.48 | 21.13 | 39.06 | 47.57 | 59.62 | 82.33 | ▂▇▆▅▂ |
| otherparty_share | 0 | 1.00 | 3.66 | 2.58 | 0.80 | 1.88 | 2.54 | 5.66 | 16.00 | ▇▂▂▁▁ |
| white_share | 0 | 1.00 | 57.83 | 19.31 | 12.67 | 40.35 | 56.92 | 75.99 | 89.98 | ▁▇▆▆▇ |
| asian_share | 0 | 1.00 | 6.03 | 6.70 | 0.21 | 1.27 | 3.58 | 7.04 | 32.82 | ▇▁▁▁▁ |
| black_share | 0 | 1.00 | 3.04 | 3.19 | 0.00 | 0.81 | 1.82 | 3.50 | 14.65 | ▇▂▁▁▁ |
| hispanic_share | 0 | 1.00 | 28.49 | 17.22 | 5.15 | 13.41 | 24.73 | 42.22 | 82.03 | ▇▆▃▂▁ |
| other_share | 0 | 1.00 | 4.61 | 2.93 | 1.55 | 2.89 | 3.75 | 5.52 | 21.52 | ▇▂▁▁▁ |
| young_drivers | 0 | 1.00 | 14.24 | 2.73 | 8.65 | 12.10 | 14.22 | 15.81 | 25.39 | ▅▇▅▁▁ |
| density | 0 | 1.00 | 364.64 | 694.47 | 1.53 | 24.97 | 100.92 | 321.29 | 4070.64 | ▇▁▁▁▁ |
| areain_square_miles | 0 | 1.00 | 2781.69 | 3096.29 | 440.00 | 1003.00 | 1598.00 | 3510.00 | 20164.00 | ▇▁▁▁▁ |
| med_inc | 0 | 1.00 | 55598.49 | 17114.92 | 28533.00 | 43237.00 | 52078.00 | 63398.00 | 139462.00 | ▇▇▂▁▁ |
| unemp | 0 | 1.00 | 8.72 | 3.99 | 2.10 | 5.70 | 8.00 | 10.70 | 28.90 | ▇▇▂▁▁ |
| own_source_share | 0 | 1.00 | 43.67 | 16.07 | 15.17 | 32.46 | 41.09 | 49.33 | 97.96 | ▃▇▃▁▁ |
| emp_goods | 0 | 1.00 | 43390.45 | 85018.15 | 0.00 | 2107.00 | 13093.00 | 47344.00 | 642230.00 | ▇▁▁▁▁ |
| emp_service | 0 | 1.00 | 175746.56 | 442315.84 | 0.00 | 6374.00 | 34955.00 | 124505.00 | 3439959.00 | ▇▁▁▁▁ |
| pay_goods_i | 0 | 1.00 | 39124.06 | 16100.25 | 0.00 | 29667.93 | 35001.89 | 43053.98 | 160212.25 | ▅▇▁▁▁ |
| pay_service_i | 0 | 1.00 | 31512.13 | 11371.71 | 0.00 | 25082.33 | 28896.69 | 34273.00 | 116676.48 | ▂▇▁▁▁ |
| arte_share | 56 | 0.95 | 1.75 | 2.30 | 0.00 | 0.60 | 1.11 | 1.83 | 17.49 | ▇▁▁▁▁ |
| collect_share | 56 | 0.95 | 1.75 | 1.85 | 0.00 | 0.80 | 1.22 | 1.94 | 14.79 | ▇▁▁▁▁ |
| cnty_le_sworn_1000p | 0 | 1.00 | 1.93 | 1.34 | 0.72 | 1.39 | 1.65 | 2.02 | 12.89 | ▇▁▁▁▁ |
| felony_tot_1000p | 0 | 1.00 | 12.70 | 4.58 | 4.08 | 9.48 | 11.97 | 15.49 | 34.35 | ▅▇▃▁▁ |
| misdemeanor_tot_1000p | 0 | 1.00 | 29.72 | 11.26 | 8.18 | 21.48 | 28.20 | 36.72 | 156.12 | ▇▂▁▁▁ |
| forfeitures_i_p | 0 | 1.00 | 3.34 | 6.06 | 0.00 | 0.43 | 1.98 | 4.61 | 154.06 | ▇▁▁▁▁ |
| other_court_fines_i_p | 0 | 1.00 | 10.81 | 16.44 | 0.00 | 2.79 | 6.36 | 11.62 | 154.86 | ▇▁▁▁▁ |
| delinquent_fines_i_p | 0 | 1.00 | 11.42 | 14.56 | 0.00 | 5.09 | 8.59 | 13.24 | 190.04 | ▇▁▁▁▁ |
| vic_margin | 807 | 0.21 | 0.12 | 0.17 | 0.00 | 0.00 | 0.00 | 0.22 | 0.97 | ▇▂▁▁▁ |
Our goal is to better understand how politicians manipulate government policy during electoral years in an effort to gain an electoral advantage. First, we are going to investigate the relationship between a county’s median household income and the per capita traffic fines revenue (adjusted for inflation) (simply referred to as per capita traffic fines revenue).
-
Question: Based on our research focus, which variable is the response variable?
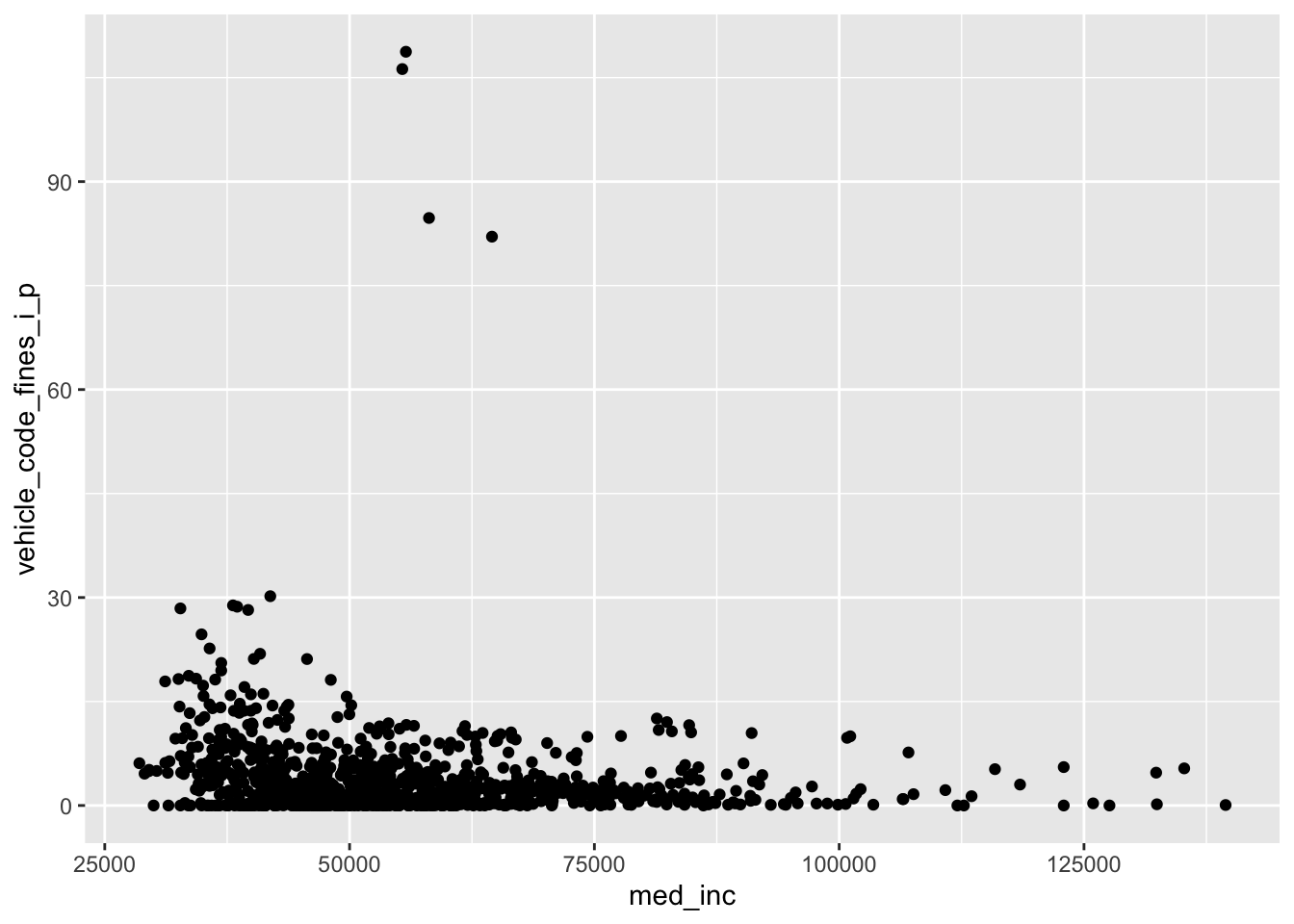
vehicle_code_fines_i_p Demo: Visualize the relationship between median household income and per capita traffic fines revenue.
ggplot(
data = traffic_fines,
mapping = aes(x = med_inc, y = vehicle_code_fines_i_p)
) +
geom_point()Correlation
- Demo: What is the correlation between median household income and per capita traffic fines revenue?
Estimate a model with a continuous explanatory variable
- Demo: Write the population model below that explains the relationship between median household income and per capita traffic fines revenue.
$$
\text{traffic fines} = \beta_0 + \beta_1 \times \text{median household income}
$$\[ \text{traffic fines} = \beta_0 + \beta_1 \times \text{median household income} \]
- Demo: Fit the linear regression model and display the results. Write the estimated model output below.
Use tidy() to print the model output in a readable, tabular format.
fines_inc_fit <- linear_reg() |>
fit(vehicle_code_fines_i_p ~ med_inc, data = traffic_fines)
tidy(fines_inc_fit)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 6.93 0.762 9.10 4.45e-19
2 med_inc -0.0000546 0.0000131 -4.17 3.35e- 5$$
\widehat{\text{traffic fines}} = 6.93 - 0.0000546 \times \text{median household income}
$$\[ \widehat{\text{traffic fines}} = 6.93 - 0.0000546 \times \text{median household income} \]
-
Your turn: Interpret the slope and the intercept in the context of the data.
Intercept: Counties with a median household income of $0, on average, earn $6.93 per capita in traffic fines revenue.
-
Slopes: For each additional dollar of median household income, the per capita traffic fines revenue is lower by $0.0000546, on average.
Alternative: For each additional $1,000 of median household income, the per capita traffic fines revenue is lower by $0.0546, on average.
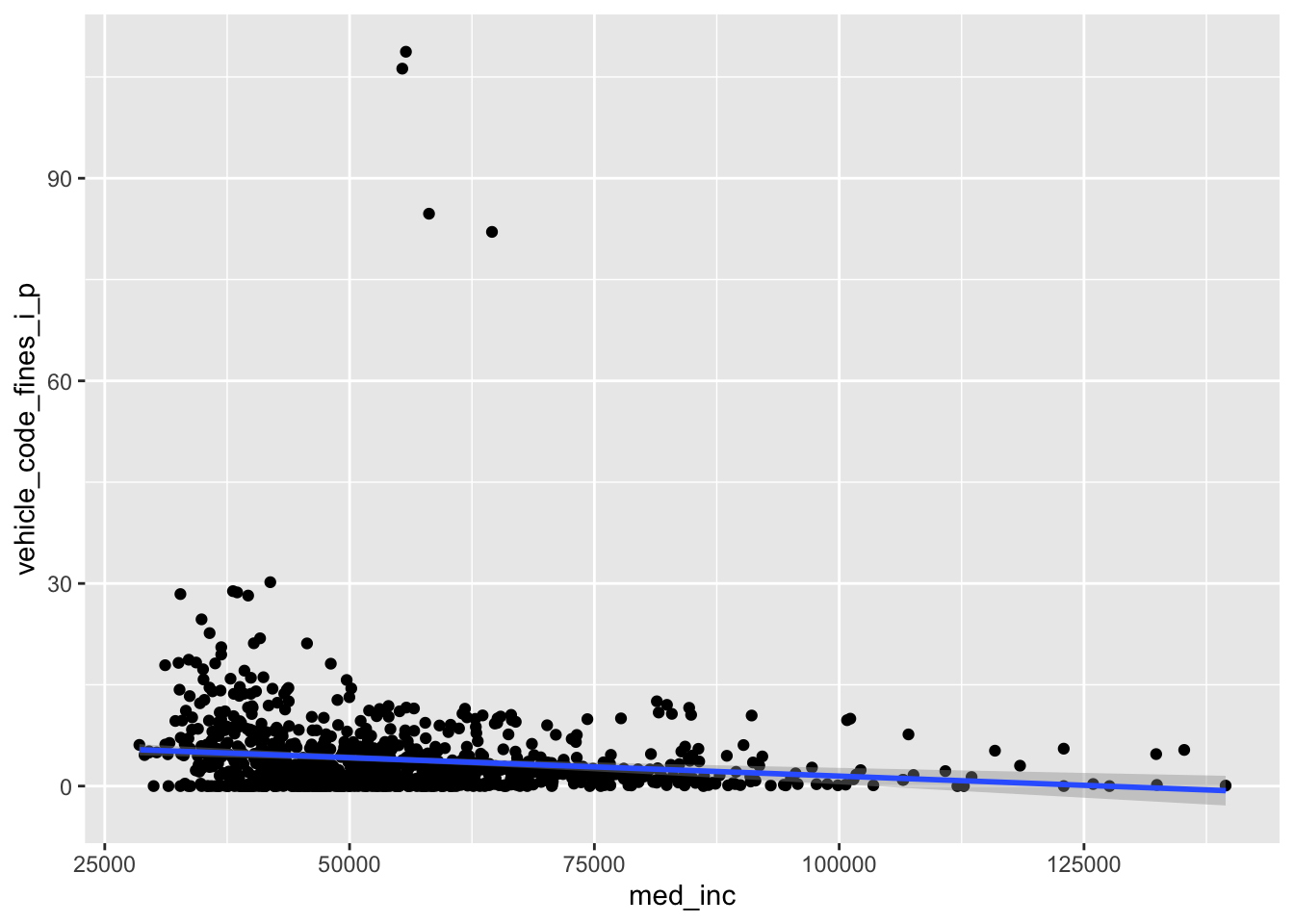
Your turn: Recreate the visualization from above, this time adding a regression line to the visualization
geom_smooth(method = "lm").
ggplot(
data = traffic_fines,
mapping = aes(x = med_inc, y = vehicle_code_fines_i_p)
) +
geom_point() +
geom_smooth(method = "lm")`geom_smooth()` using formula = 'y ~ x'Generate predictions
- Your turn: What is the estimated per capita traffic fines revenue for a county with $80,000 median household income?
Use predict() to generate predicted values from a fitted model. Provide the new data in a data frame as the new_data argument.
- Your turn: What is the estimated per capita traffic fines revenue for a county with $15,000 median household income?
But we shouldn’t do this prediction based on this model since $15,000 is outside of the range of the data (extrapolation).
Conduct a hypothesis test
-
Your turn: State the hypotheses to evaluate the relationship between median household income and per capita traffic fines revenue.
-
Null hypothesis: There is no linear relationship between median household income and per capita traffic fines revenue.
\[H_0: \beta_1 = 0\]
-
Alternative hypothesis: There is some linear relationship between median household income and per capita traffic fines revenue.
\[H_A: \beta_1 \neq 0\]
-
Demo: Use permutation-based methods to conduct the hypothesis test.
# calculate observed fit
obs_fit <- traffic_fines |>
specify(vehicle_code_fines_i_p ~ med_inc) |>
fit()
# generate permuted null distribution
null_dist <- traffic_fines |>
specify(vehicle_code_fines_i_p ~ med_inc) |>
hypothesize(null = "independence") |>
generate(reps = 1000, type = "permute") |>
fit()
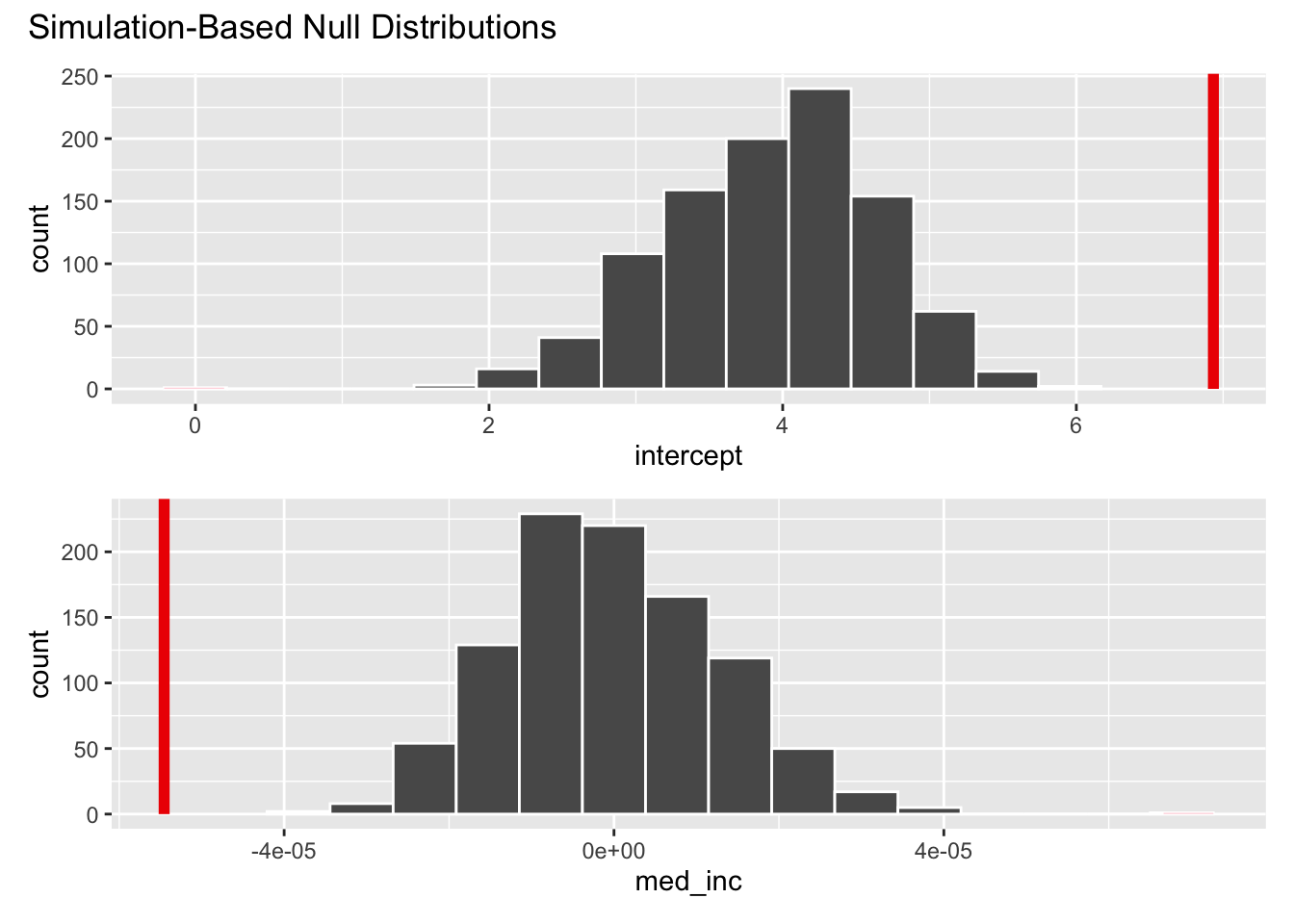
# visualize and calculate p-value
visualize(null_dist) +
shade_p_value(obs_fit, direction = "both")get_p_value(null_dist, obs_fit, direction = "both")Warning: Please be cautious in reporting a p-value of 0. This result is an approximation
based on the number of `reps` chosen in the `generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.
Please be cautious in reporting a p-value of 0. This result is an approximation
based on the number of `reps` chosen in the `generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.# A tibble: 2 × 2
term p_value
<chr> <dbl>
1 intercept 0
2 med_inc 0Your turn: Interpret the \(p\)-value in context of the data and the research question. Use a significance level of 5%.
Add response here. If in fact the true relationship between median household income and per capita traffic fines revenue is zero, the probability of observing a relationship as strong as the one in the data is less than 0.001. Since this is less than 0.05, we reject the null hypothesis and conclude that there is a relationship between median household income and per capita traffic fines revenue.
Estimate bootstrap confidence intervals for the slope
- Demo: Estimate the 95% confidence interval for the slope of the relationship between median household income and per capita traffic fines revenue.
# bootstrap distribution for CIs
boot_full_dist <- traffic_fines |>
specify(vehicle_code_fines_i_p ~ med_inc) |>
generate(reps = 1000, type = "bootstrap") |>
fit()
# get 95% confidence interval
conf_ints <- get_ci(boot_full_dist, level = 0.95, point_estimate = obs_fit)
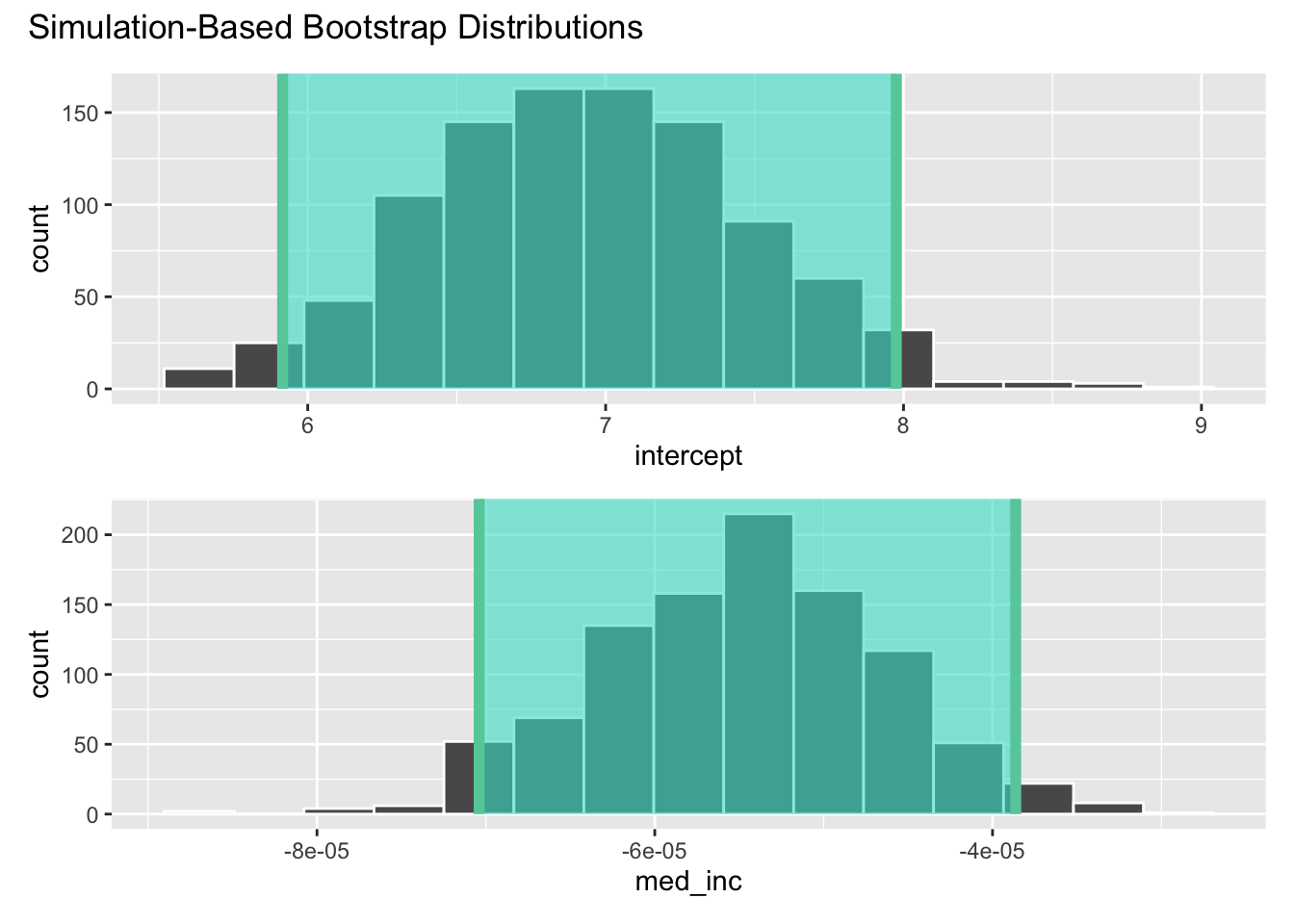
visualize(boot_full_dist) +
shade_confidence_interval(conf_ints)Your turn: How do we interpret this confidence interval?
Add response here. We are 95% confident that the true slope of the relationship between median household income and per capita traffic fines revenue is between \(-0.0000717\) and \(-0.0000399\).
Another model with a categorical explanatory variable
-
Your turn: Now we are prepared to ask the question we most care about: do politicians manipulate government policy during electoral years in an effort to gain an electoral advantage? In order to answer the question, we will examine the relationship between whether or not a sheriff election is held in the year and per capita traffic fines revenue.
Response variable:
vehicle_code_fines_i_pPredictor variable:
sheriff_electionPredictor type: Categorical
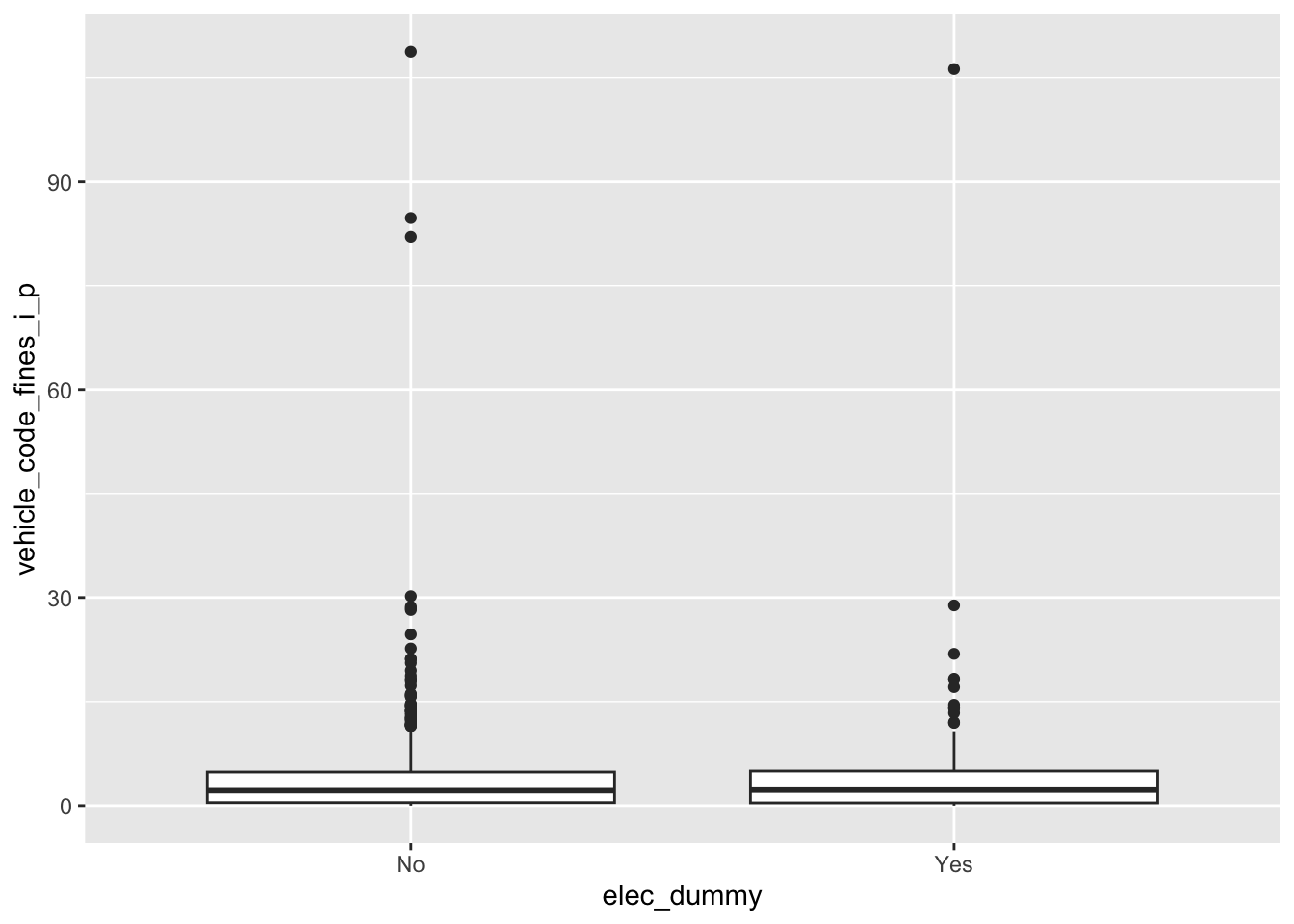
Demo: Make an appropriate visualization to investigate this relationship below. Additionally, calculate the mean per capita traffic fines revenue for years that are and are not election years.
Choose a visualization appropriate for a categorical and continuous variable.
ggplot(
data = traffic_fines,
mapping = aes(x = elec_dummy, y = vehicle_code_fines_i_p)
) +
geom_boxplot()traffic_fines |>
group_by(elec_dummy) |>
summarize(mean_fines = mean(vehicle_code_fines_i_p, na.rm = TRUE))# A tibble: 2 × 2
elec_dummy mean_fines
<chr> <dbl>
1 No 3.90
2 Yes 3.91-
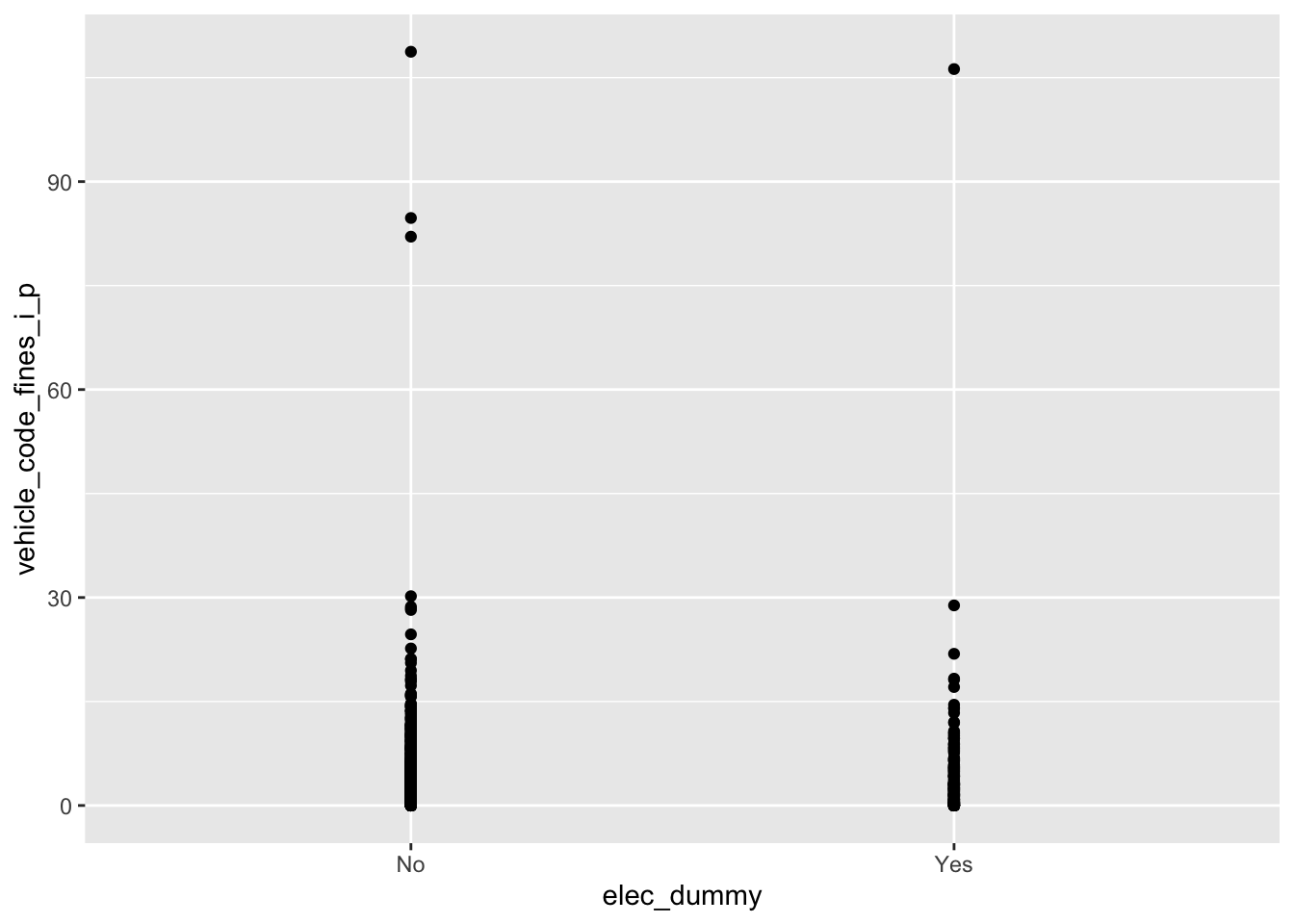
Demo: Change the geom of your previous plot to
geom_point(). Use this plot to think about how R models these data.
ggplot(
data = traffic_fines,
mapping = aes(x = elec_dummy, y = vehicle_code_fines_i_p)
) +
geom_point()- Your turn: Fit the linear regression model and display the results. Print the estimated model output below.
fines_elec_dummy_fit <- linear_reg() |>
fit(vehicle_code_fines_i_p ~ elec_dummy, data = traffic_fines)
tidy(fines_elec_dummy_fit)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 3.90 0.256 15.2 2.84e-47
2 elec_dummyYes 0.0171 0.543 0.0315 9.75e- 1-
Demo: Interpret the slope and the intercept in the context of the data.
Intercept: Counties not in an election year are expected to earn, on average, $3.90 per capita in traffic fines revenue.
Slope: Counties in an election year are expected to earn, on average, $0.02 less per capita in traffic fines revenue than those not in an election year.
Conduct a hypothesis test
-
Your turn: State the hypotheses to evaluate the relationship between median household income and per capita traffic fines revenue.
-
Null hypothesis: There is no linear relationship between whether or not it is an election year and per capita traffic fines revenue.
\[H_0: \beta_1 = 0\]
-
Alternative hypothesis: There is some linear relationship between whether or not it is an election year and per capita traffic fines revenue.
\[H_A: \beta_1 \neq 0\]
-
Demo: Use permutation-based methods to conduct the hypothesis test.
# calculate observed fit
obs_fit <- traffic_fines |>
specify(vehicle_code_fines_i_p ~ elec_dummy) |>
fit()
# generate permuted null distribution
null_dist <- traffic_fines |>
specify(vehicle_code_fines_i_p ~ elec_dummy) |>
hypothesize(null = "independence") |>
generate(reps = 1000, type = "permute") |>
fit()
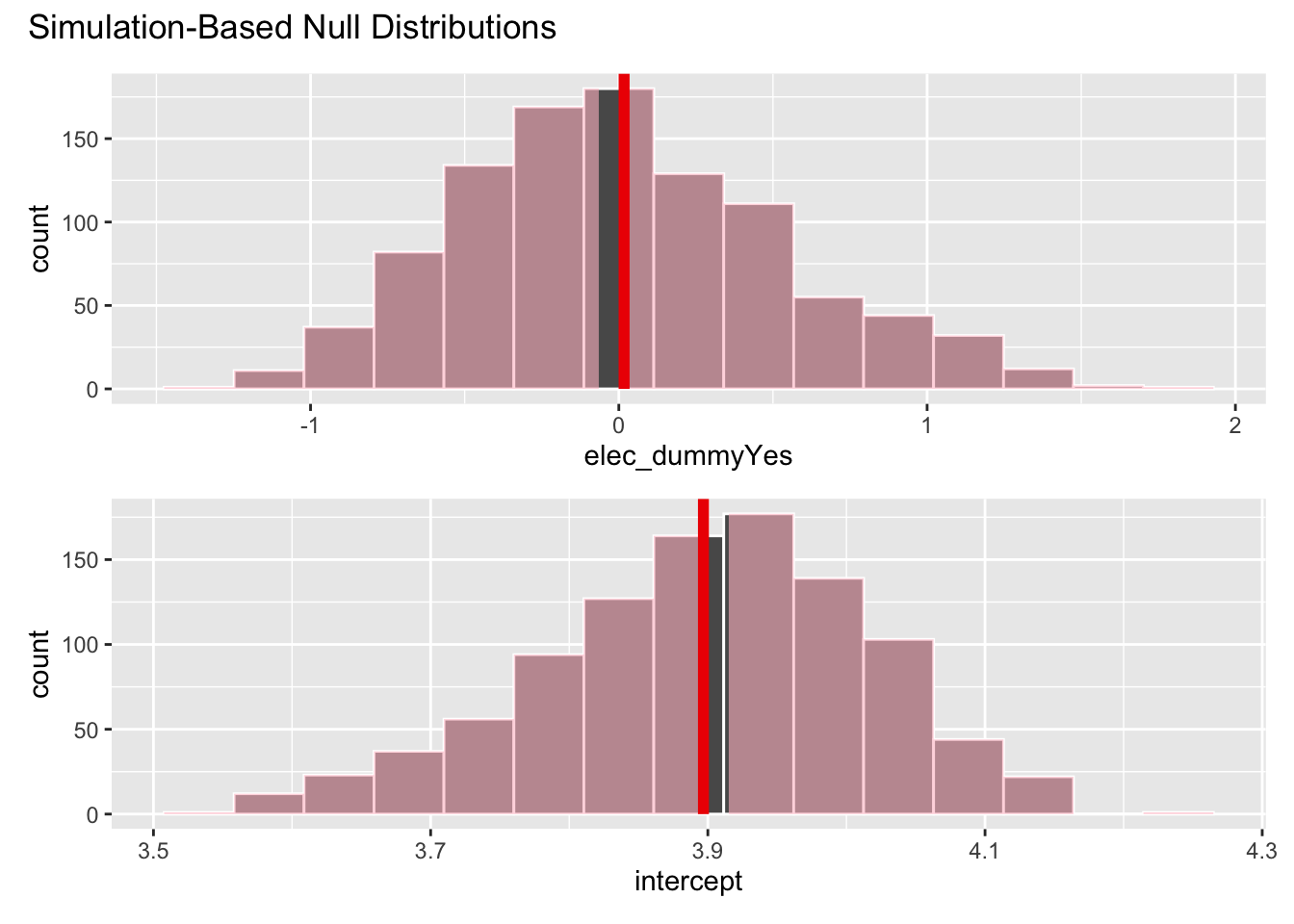
# visualize and calculate p-value
visualize(null_dist) +
shade_p_value(obs_fit, direction = "both")get_p_value(null_dist, obs_fit, direction = "both")# A tibble: 2 × 2
term p_value
<chr> <dbl>
1 elec_dummyYes 0.942
2 intercept 0.942Your turn: Interpret the \(p\)-value in context of the data and the research question. Use a significance level of 5%.
Add response here. If in fact the true relationship between whether or not it is an election and per capita traffic fines revenue is zero, the probability of observing a relationship as strong as the one in the data is less than 0.95. Since this is greater than 0.05, we fail to reject the null hypothesis and cannot conclude that there is a relationship between whether or not it is an election and per capita traffic fines revenue.
Check model conditions
Recall the technical conditions for linear regression:
- L: linear model
- I: independent observations
- N: points are normally distributed around the line
- E: equal variability around the line for all values of the explanatory variable
Your turn: Check the linearity assumption for the model with elec_dummy as the predictor. Examine the residuals to assist you with this process.
# augment() allows us to extract observation-level statistics from a model object
fines_elec_dummy_aug <- augment(fines_elec_dummy_fit, new_data = traffic_fines)
fines_elec_dummy_aug# A tibble: 1,025 × 40
.pred .resid year county_code county_name vehicle_code_fines
<dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 3.90 -0.507 2003 1 Alameda 4973766
2 3.90 -0.107 2004 1 Alameda 5701454
3 3.90 -0.899 2005 1 Alameda 4645572
4 3.91 -0.639 2006 1 Alameda 5256212
5 3.90 -0.591 2007 1 Alameda 5498544
6 3.90 -0.388 2008 1 Alameda 6124421
7 3.90 -0.276 2009 1 Alameda 6346925
8 3.91 -0.713 2010 1 Alameda 5753802
9 3.90 -1.15 2011 1 Alameda 5154709
10 3.90 -1.63 2012 1 Alameda 4409751
# ℹ 1,015 more rows
# ℹ 34 more variables: vehicle_code_fines_i_p <dbl>, elec_dummy <chr>,
# sheriff_incumb <dbl>, pre_elec <dbl>, no_incumb <dbl>, incumb <dbl>,
# sheriff_margin <dbl>, rep_share <dbl>, dem_share <dbl>,
# otherparty_share <dbl>, white_share <dbl>, asian_share <dbl>,
# black_share <dbl>, hispanic_share <dbl>, other_share <dbl>,
# young_drivers <dbl>, density <dbl>, areain_square_miles <dbl>, …# the linear regression model
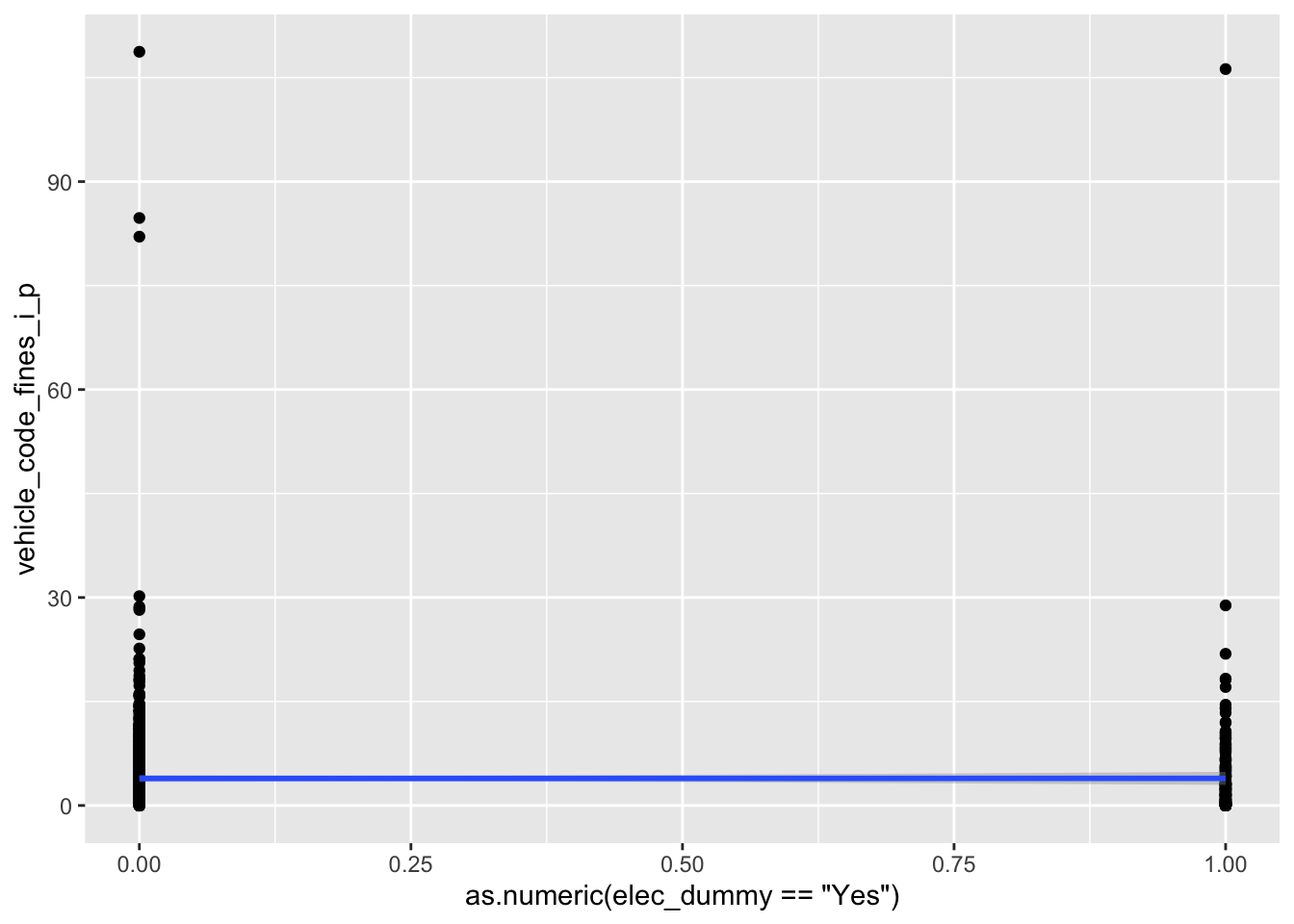
ggplot(
data = fines_elec_dummy_aug,
mapping = aes(
x = as.numeric(elec_dummy == "Yes"),
y = vehicle_code_fines_i_p
)
) +
geom_point() +
geom_smooth(method = "lm")`geom_smooth()` using formula = 'y ~ x'# distribution of the residuals
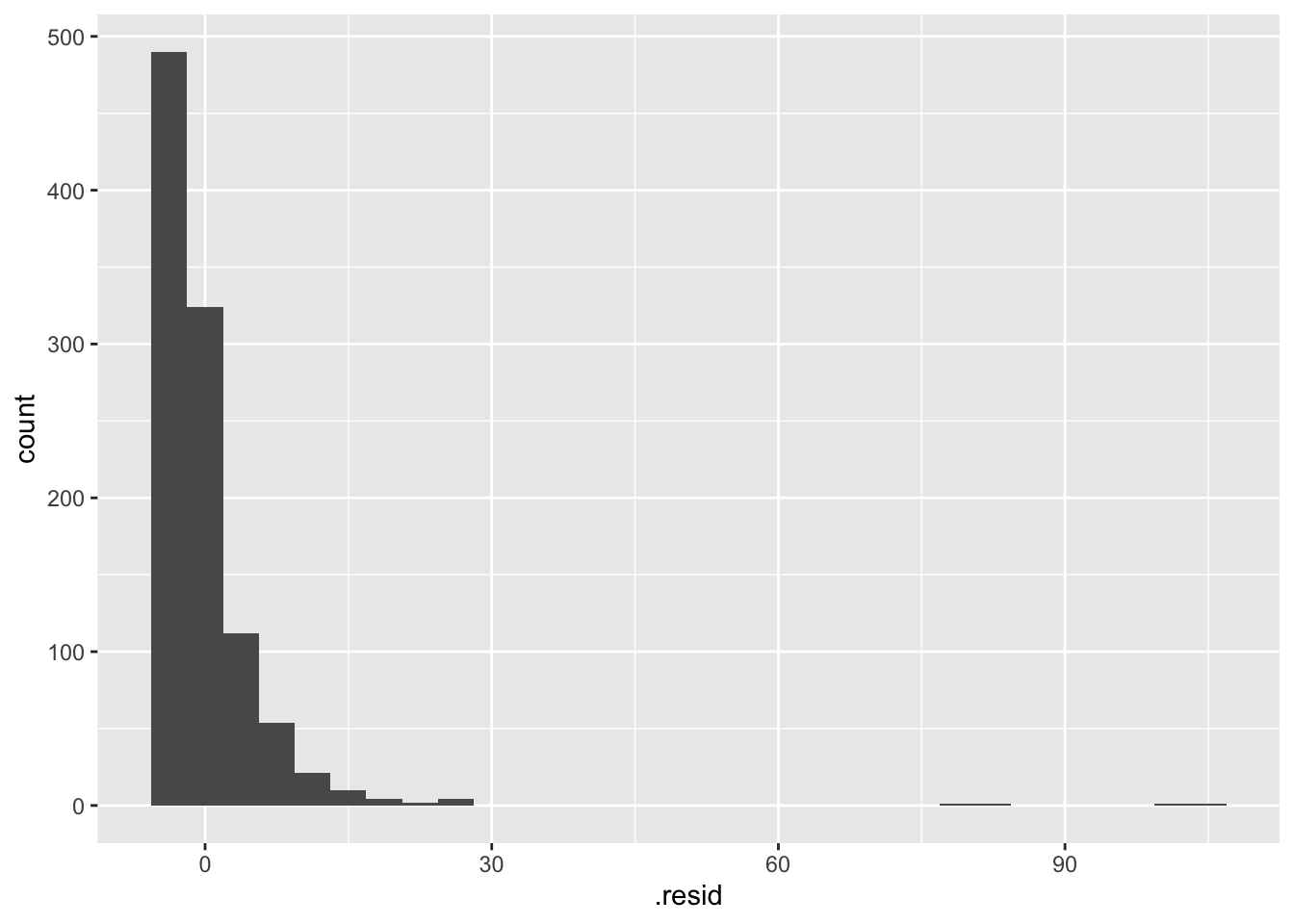
ggplot(data = fines_elec_dummy_aug, mapping = aes(x = .resid)) +
geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.# use the .resid column to plot the predicted values vs. the residuals
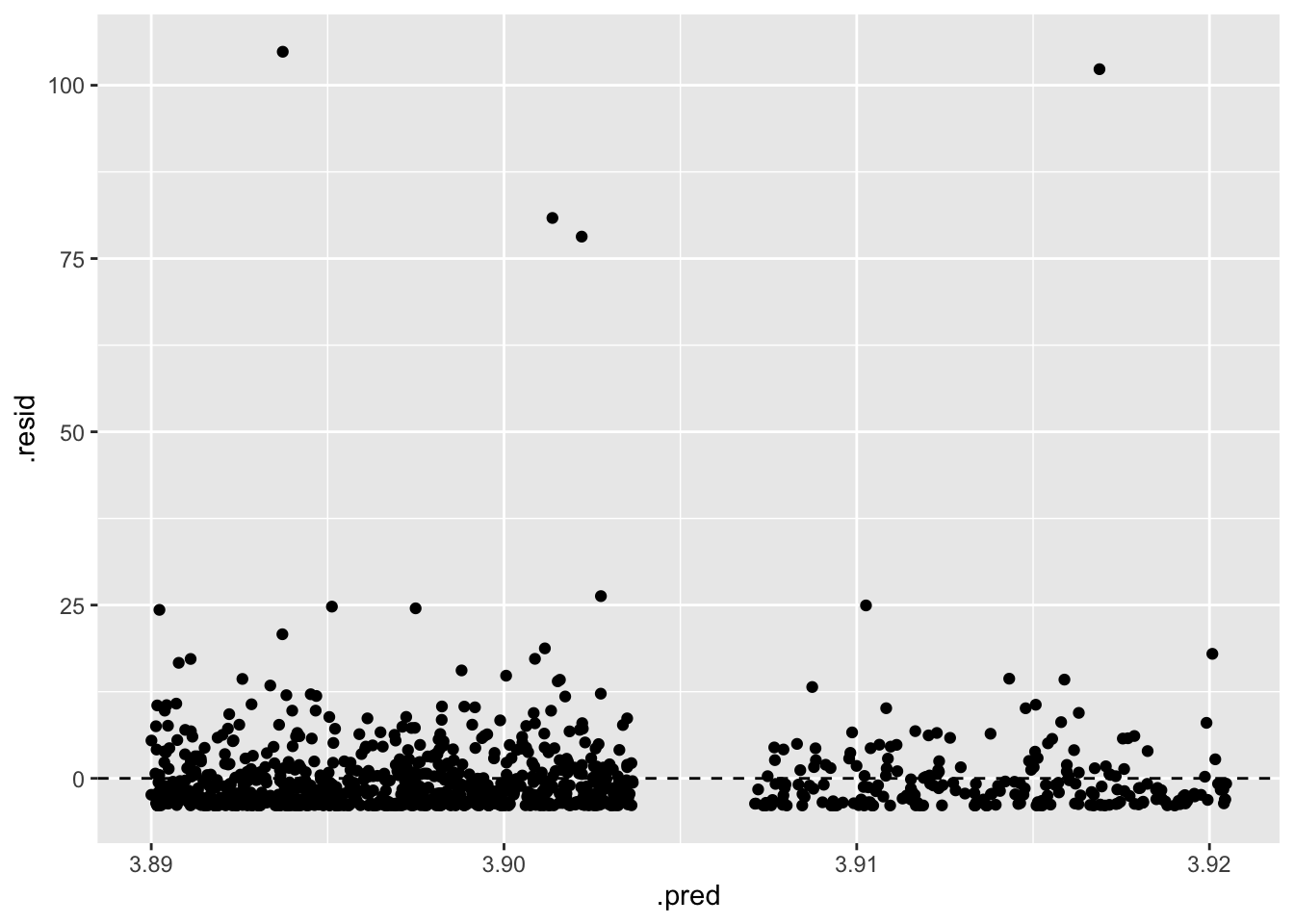
# jitter because the explanatory variable only has 2 unique values
ggplot(data = fines_elec_dummy_aug, mapping = aes(x = .pred, y = .resid)) +
geom_jitter() +
geom_hline(yintercept = 0, linetype = "dashed")-
L: linear model - Add response here.
Doesn’t seem very linear in the relationship. The fact that we have a categorical variable as the predictor is not inherently a problem, but it doesn’t seem like there is a straight, monotonic relationship between the predictor and the response.
-
I: independent observations - Add response here.
Absolutely no. There are many reasons why the observations are not independent. The obvious reason is that it is a time series cross-sectional (TSCS) panel structure. Each county is observed over multiple years, and the observations within a county are likely to be correlated. Alternatively, each year is observed over multiple counties, and the observations within a year are likely to be correlated.
-
N: points are normally distributed around the line - Add response here.
No. The boxplot earlier shows there are many outliers in the data. The residuals are not normally distributed around the line.
-
E: equal variability around the line for all values of the explanatory variable - Add response here.
No. The residuals are not equally variable around the line for all values of the explanatory variable. The residuals are more variable for counties in an election year than for counties not in an election year.
sessioninfo::session_info()─ Session info ───────────────────────────────────────────────────────────────
setting value
version R version 4.4.2 (2024-10-31)
os macOS Sonoma 14.6.1
system aarch64, darwin20
ui X11
language (EN)
collate en_US.UTF-8
ctype en_US.UTF-8
tz America/New_York
date 2025-03-26
pandoc 3.4 @ /usr/local/bin/ (via rmarkdown)
─ Packages ───────────────────────────────────────────────────────────────────
package * version date (UTC) lib source
archive 1.1.9 2024-09-12 [1] CRAN (R 4.4.1)
backports 1.5.0 2024-05-23 [1] CRAN (R 4.4.0)
base64enc 0.1-3 2015-07-28 [1] CRAN (R 4.3.0)
bit 4.0.5 2022-11-15 [1] CRAN (R 4.3.0)
bit64 4.0.5 2020-08-30 [1] CRAN (R 4.3.0)
broom * 1.0.6 2024-05-17 [1] CRAN (R 4.4.0)
class 7.3-22 2023-05-03 [1] CRAN (R 4.4.2)
cli 3.6.3 2024-06-21 [1] CRAN (R 4.4.0)
codetools 0.2-20 2024-03-31 [1] CRAN (R 4.4.2)
crayon 1.5.3 2024-06-20 [1] CRAN (R 4.4.0)
data.table 1.15.4 2024-03-30 [1] CRAN (R 4.3.1)
dials * 1.3.0 2024-07-30 [1] CRAN (R 4.4.0)
DiceDesign 1.10 2023-12-07 [1] CRAN (R 4.3.1)
dichromat 2.0-0.1 2022-05-02 [1] CRAN (R 4.3.0)
digest 0.6.37 2024-08-19 [1] CRAN (R 4.4.1)
dplyr * 1.1.4 2023-11-17 [1] CRAN (R 4.3.1)
evaluate 1.0.3 2025-01-10 [1] CRAN (R 4.4.1)
farver 2.1.2 2024-05-13 [1] CRAN (R 4.3.3)
fastmap 1.2.0 2024-05-15 [1] CRAN (R 4.4.0)
forcats * 1.0.0 2023-01-29 [1] CRAN (R 4.3.0)
foreach 1.5.2 2022-02-02 [1] CRAN (R 4.3.0)
furrr 0.3.1 2022-08-15 [1] CRAN (R 4.3.0)
future 1.33.2 2024-03-26 [1] CRAN (R 4.3.1)
future.apply 1.11.2 2024-03-28 [1] CRAN (R 4.3.1)
generics 0.1.3 2022-07-05 [1] CRAN (R 4.3.0)
ggplot2 * 3.5.1 2024-04-23 [1] CRAN (R 4.3.1)
globals 0.16.3 2024-03-08 [1] CRAN (R 4.3.1)
glue 1.8.0 2024-09-30 [1] CRAN (R 4.4.1)
gower 1.0.1 2022-12-22 [1] CRAN (R 4.3.0)
GPfit 1.0-8 2019-02-08 [1] CRAN (R 4.3.0)
gtable 0.3.6 2024-10-25 [1] CRAN (R 4.4.1)
hardhat 1.4.0 2024-06-02 [1] CRAN (R 4.4.0)
here 1.0.1 2020-12-13 [1] CRAN (R 4.3.0)
hms 1.1.3 2023-03-21 [1] CRAN (R 4.3.0)
htmltools 0.5.8.1 2024-04-04 [1] CRAN (R 4.3.1)
htmlwidgets 1.6.4 2023-12-06 [1] CRAN (R 4.3.1)
infer * 1.0.7 2024-03-25 [1] CRAN (R 4.3.1)
ipred 0.9-14 2023-03-09 [1] CRAN (R 4.3.0)
iterators 1.0.14 2022-02-05 [1] CRAN (R 4.3.0)
jsonlite 1.8.9 2024-09-20 [1] CRAN (R 4.4.1)
knitr 1.49 2024-11-08 [1] CRAN (R 4.4.1)
labeling 0.4.3 2023-08-29 [1] CRAN (R 4.3.0)
lattice 0.22-6 2024-03-20 [1] CRAN (R 4.4.2)
lava 1.8.0 2024-03-05 [1] CRAN (R 4.3.1)
lhs 1.1.6 2022-12-17 [1] CRAN (R 4.3.0)
lifecycle 1.0.4 2023-11-07 [1] CRAN (R 4.3.1)
listenv 0.9.1 2024-01-29 [1] CRAN (R 4.3.1)
lubridate * 1.9.3 2023-09-27 [1] CRAN (R 4.3.1)
magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.3.0)
MASS 7.3-61 2024-06-13 [1] CRAN (R 4.4.2)
Matrix 1.7-1 2024-10-18 [1] CRAN (R 4.4.2)
mgcv 1.9-1 2023-12-21 [1] CRAN (R 4.4.2)
modeldata * 1.4.0 2024-06-19 [1] CRAN (R 4.4.0)
nlme 3.1-166 2024-08-14 [1] CRAN (R 4.4.2)
nnet 7.3-19 2023-05-03 [1] CRAN (R 4.4.2)
parallelly 1.37.1 2024-02-29 [1] CRAN (R 4.3.1)
parsnip * 1.2.1 2024-03-22 [1] CRAN (R 4.3.1)
patchwork 1.2.0 2024-01-08 [1] CRAN (R 4.3.1)
pillar 1.10.1 2025-01-07 [1] CRAN (R 4.4.1)
pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.3.0)
prodlim 2023.08.28 2023-08-28 [1] CRAN (R 4.3.0)
purrr * 1.0.2 2023-08-10 [1] CRAN (R 4.3.0)
R6 2.5.1 2021-08-19 [1] CRAN (R 4.3.0)
RColorBrewer 1.1-3 2022-04-03 [1] CRAN (R 4.3.0)
Rcpp 1.0.14 2025-01-12 [1] CRAN (R 4.4.1)
readr * 2.1.5 2024-01-10 [1] CRAN (R 4.3.1)
recipes * 1.0.10 2024-02-18 [1] CRAN (R 4.3.1)
repr 1.1.7 2024-03-22 [1] CRAN (R 4.4.0)
rlang 1.1.5 2025-01-17 [1] CRAN (R 4.4.1)
rmarkdown 2.29 2024-11-04 [1] CRAN (R 4.4.1)
rpart 4.1.23 2023-12-05 [1] CRAN (R 4.4.2)
rprojroot 2.0.4 2023-11-05 [1] CRAN (R 4.3.1)
rsample * 1.2.1 2024-03-25 [1] CRAN (R 4.3.1)
rstudioapi 0.17.0 2024-10-16 [1] CRAN (R 4.4.1)
scales * 1.3.0.9000 2025-03-19 [1] Github (bensoltoff/scales@71d8f13)
sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.3.0)
skimr * 2.1.5 2022-12-23 [1] CRAN (R 4.3.0)
stringi 1.8.4 2024-05-06 [1] CRAN (R 4.3.1)
stringr * 1.5.1 2023-11-14 [1] CRAN (R 4.3.1)
survival 3.7-0 2024-06-05 [1] CRAN (R 4.4.2)
tibble * 3.2.1 2023-03-20 [1] CRAN (R 4.3.0)
tidymodels * 1.2.0 2024-03-25 [1] CRAN (R 4.3.1)
tidyr * 1.3.1 2024-01-24 [1] CRAN (R 4.3.1)
tidyselect 1.2.1 2024-03-11 [1] CRAN (R 4.3.1)
tidyverse * 2.0.0 2023-02-22 [1] CRAN (R 4.3.0)
timechange 0.3.0 2024-01-18 [1] CRAN (R 4.3.1)
timeDate 4032.109 2023-12-14 [1] CRAN (R 4.3.1)
tune * 1.2.1 2024-04-18 [1] CRAN (R 4.3.1)
tzdb 0.4.0 2023-05-12 [1] CRAN (R 4.3.0)
utf8 1.2.4 2023-10-22 [1] CRAN (R 4.3.1)
vctrs 0.6.5 2023-12-01 [1] CRAN (R 4.3.1)
vroom 1.6.5 2023-12-05 [1] CRAN (R 4.3.1)
withr 3.0.2 2024-10-28 [1] CRAN (R 4.4.1)
workflows * 1.1.4 2024-02-19 [1] CRAN (R 4.4.0)
workflowsets * 1.1.0 2024-03-21 [1] CRAN (R 4.3.1)
xfun 0.50.5 2025-01-15 [1] https://yihui.r-universe.dev (R 4.4.2)
yaml 2.3.10 2024-07-26 [1] CRAN (R 4.4.0)
yardstick * 1.3.1 2024-03-21 [1] CRAN (R 4.3.1)
[1] /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/library
──────────────────────────────────────────────────────────────────────────────