# A tibble: 146 × 3
film critics audience
<chr> <int> <int>
1 Avengers: Age of Ultron 74 86
2 Cinderella 85 80
3 Ant-Man 80 90
4 Do You Believe? 18 84
5 Hot Tub Time Machine 2 14 28
6 The Water Diviner 63 62
7 Irrational Man 42 53
8 Top Five 86 64
9 Shaun the Sheep Movie 99 82
10 Love & Mercy 89 87
# ℹ 136 more rowsLinear regression with a single predictor
Lecture 18
Cornell University
INFO 2951 - Spring 2025
March 25, 2025
Announcements
Announcements
- Homework 06
- Project EDA
- Extra credit
Modeling
Modeling
- Use models to explain the relationship between variables and to make predictions
- Many different types of models
- Linear models – classic forms used for statistical inference
- Nonlinear models – much more common in machine learning for prediction
Modeling vocabulary
- Predictor/feature/explanatory variable/independent variable
- Outcome/dependent variable/response variable
- Correlation
- Regression line (for linear models)
- Slope
- Intercept
Data overview
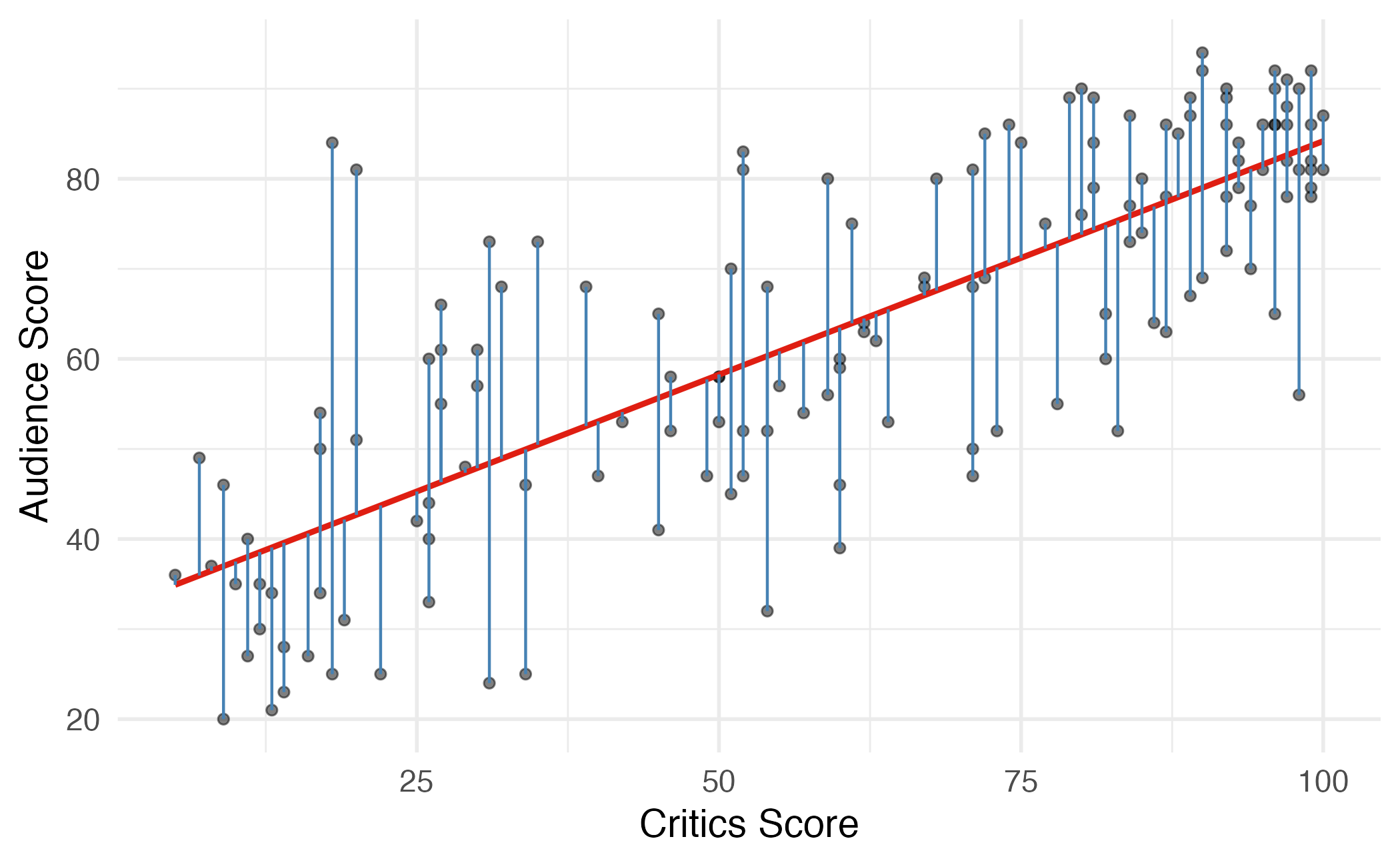
Modeling film ratings
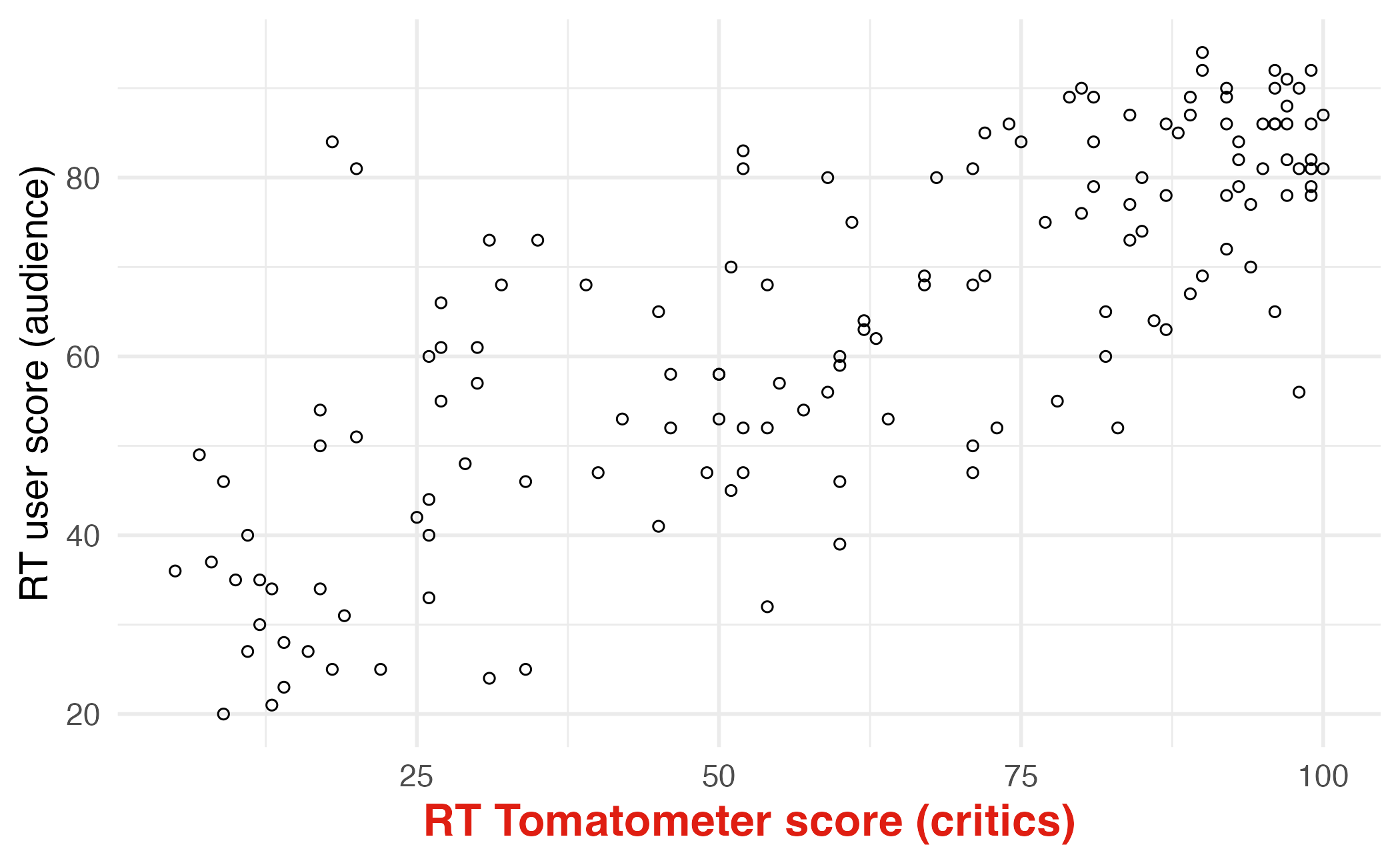
- What is the relationship between the critics and audience scores for films?
- What is your best guess for a film’s audience score if the critics rated it a 73?

Predictor (explanatory variable)
| audience | critics |
|---|---|
| 86 | 74 |
| 80 | 85 |
| 90 | 80 |
| 84 | 18 |
| 28 | 14 |
| 62 | 63 |
| ... | ... |
Outcome (response variable)
| audience | critics |
|---|---|
| 86 | 74 |
| 80 | 85 |
| 90 | 80 |
| 84 | 18 |
| 28 | 14 |
| 62 | 63 |
| ... | ... |
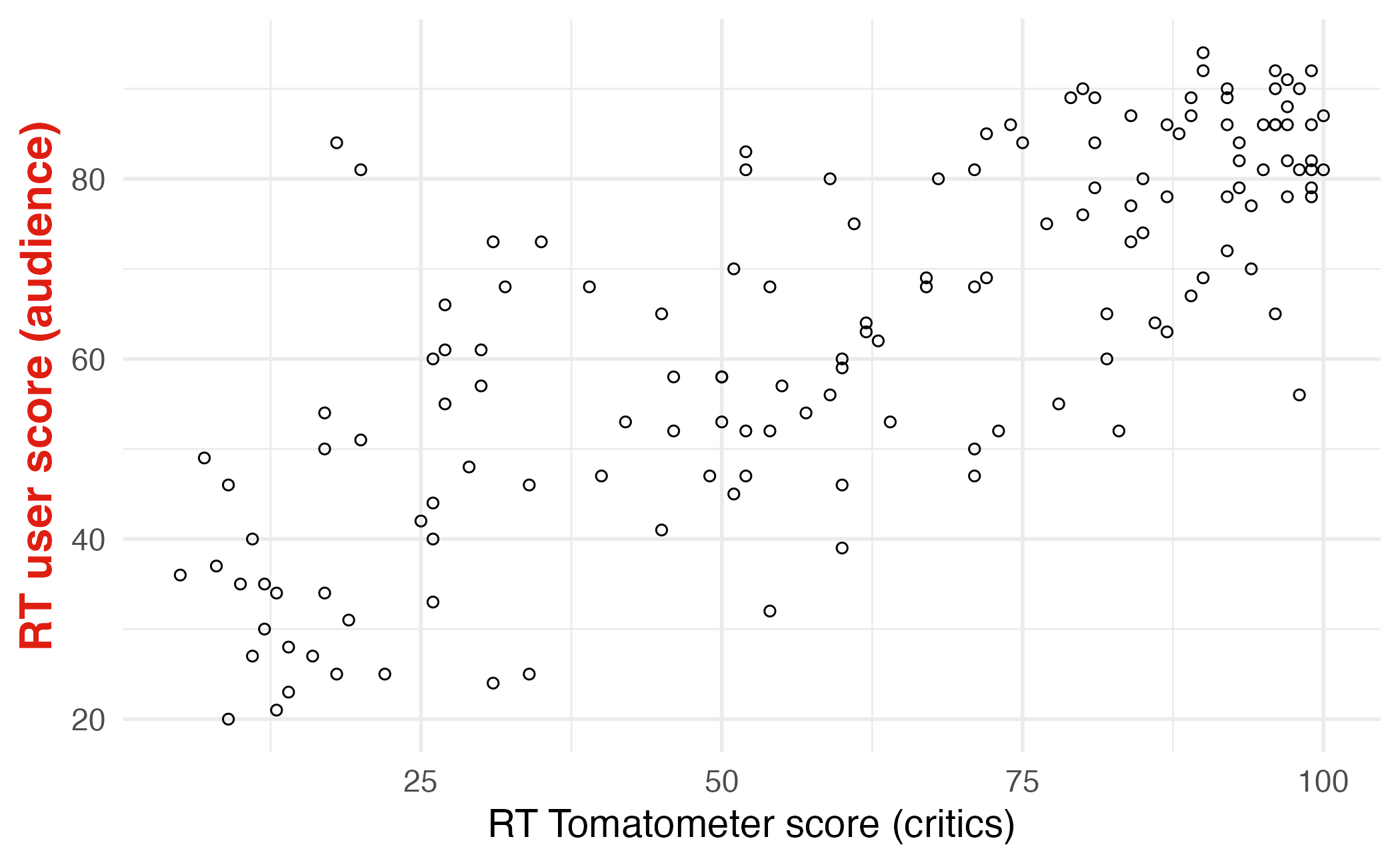
Regression line
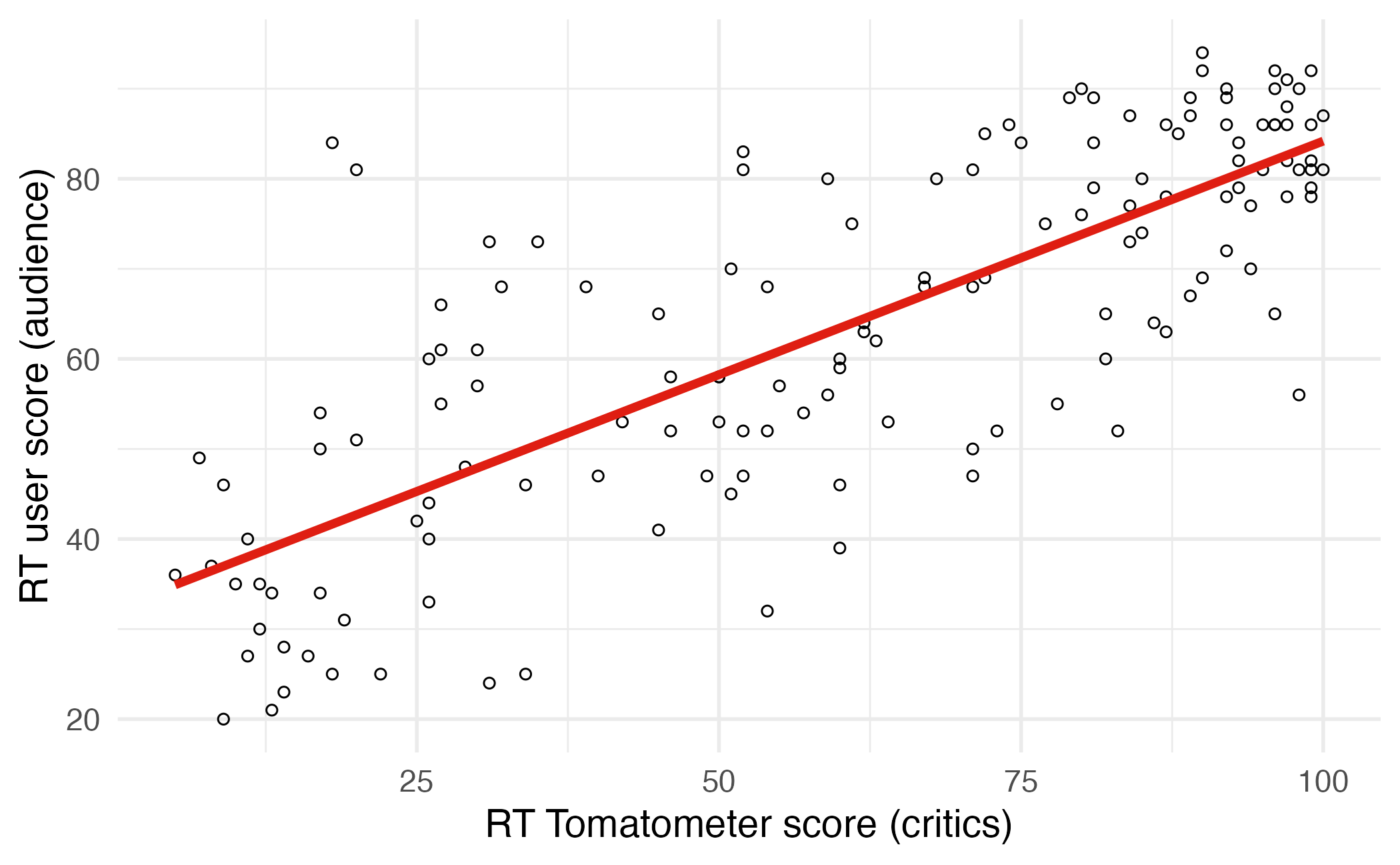
Regression line: slope

Regression line: intercept
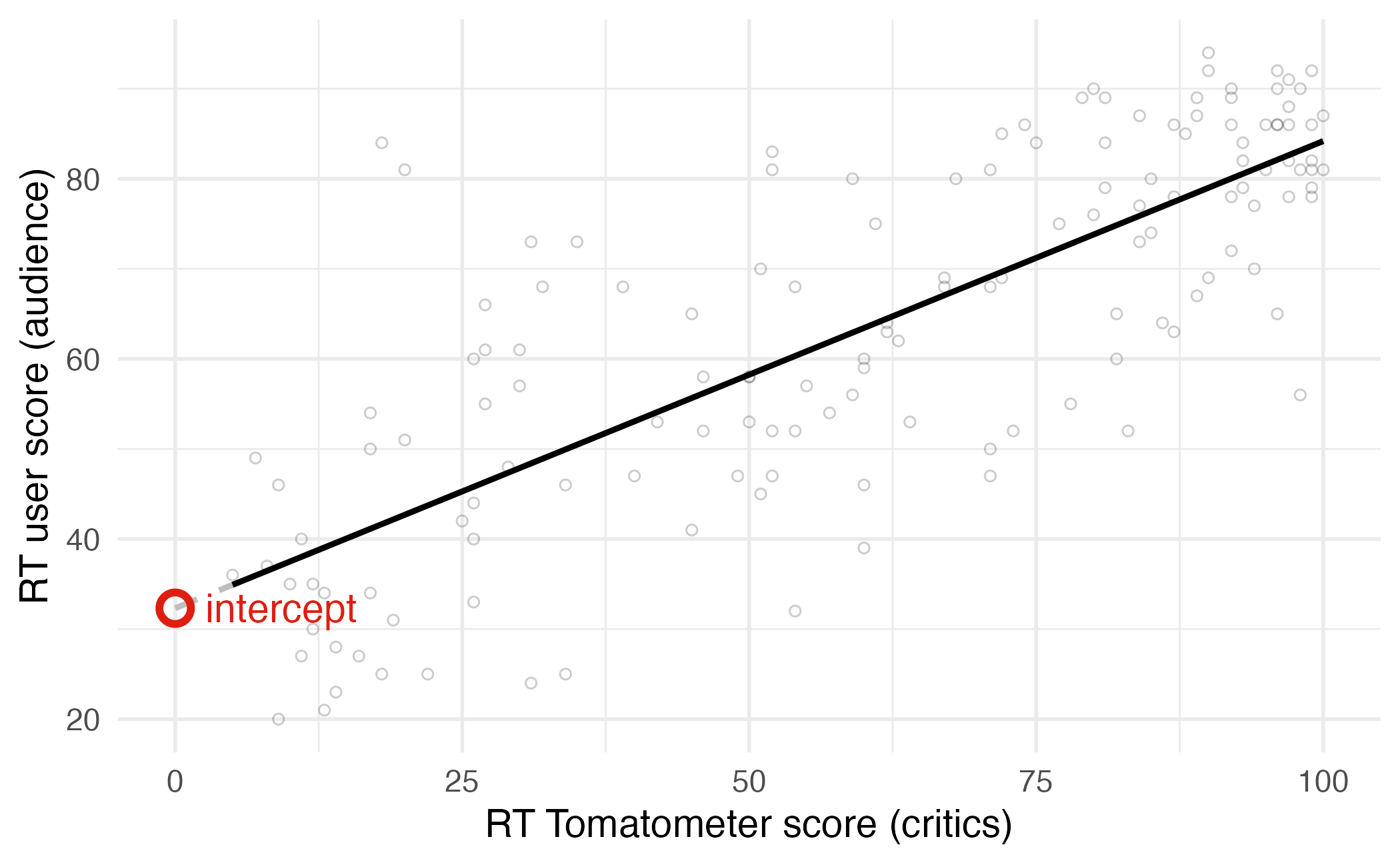
Correlation
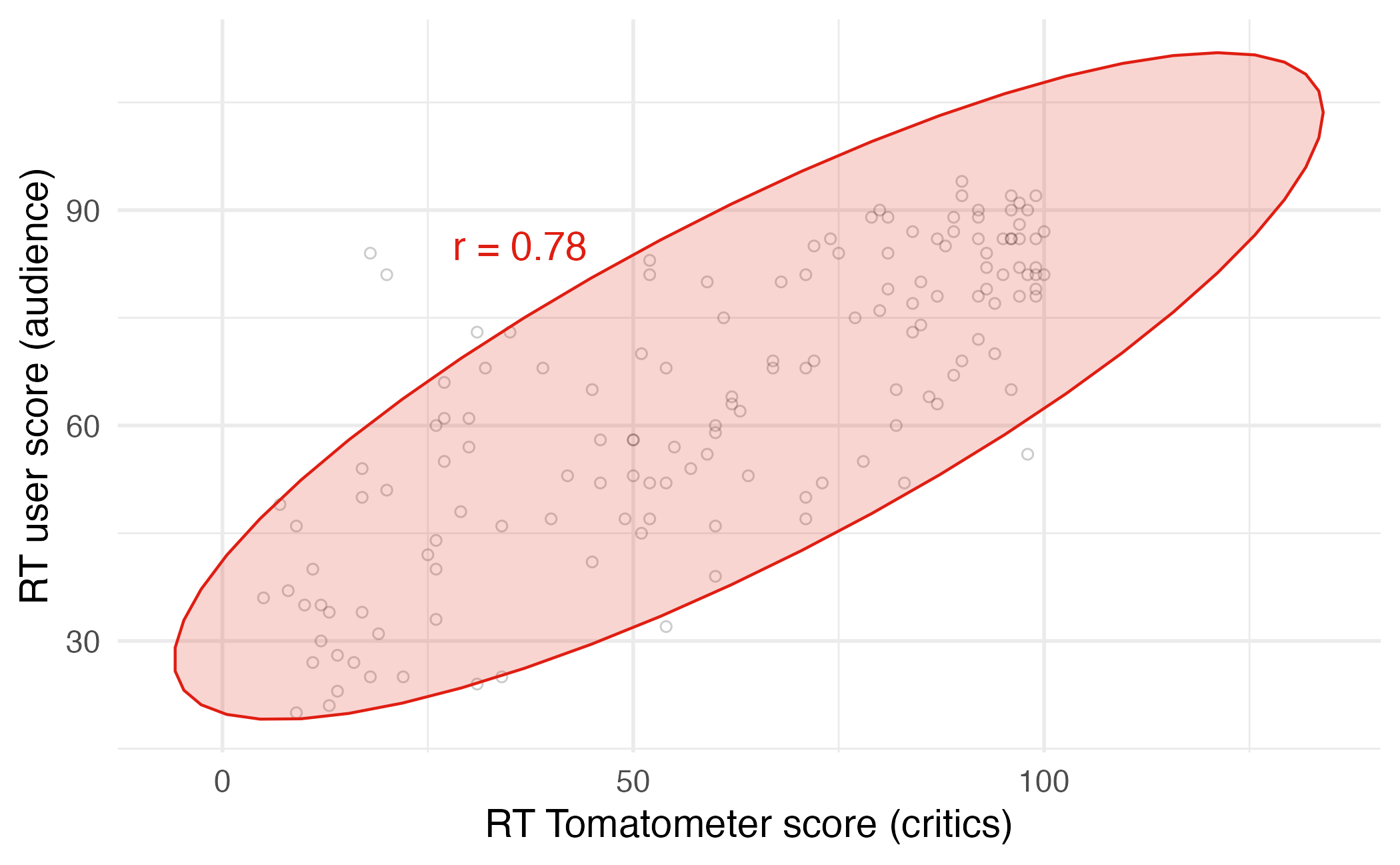
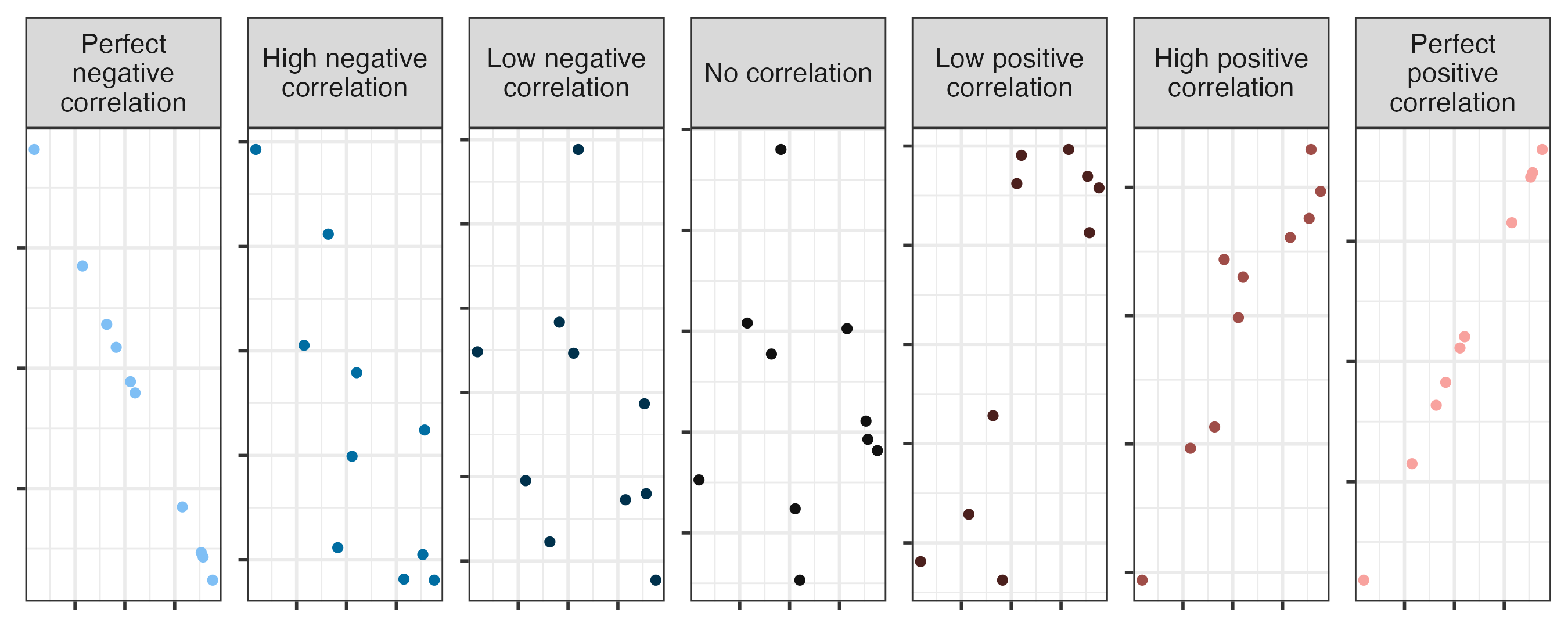
Correlation
- Ranges between -1 and 1.
- Same sign as the slope.
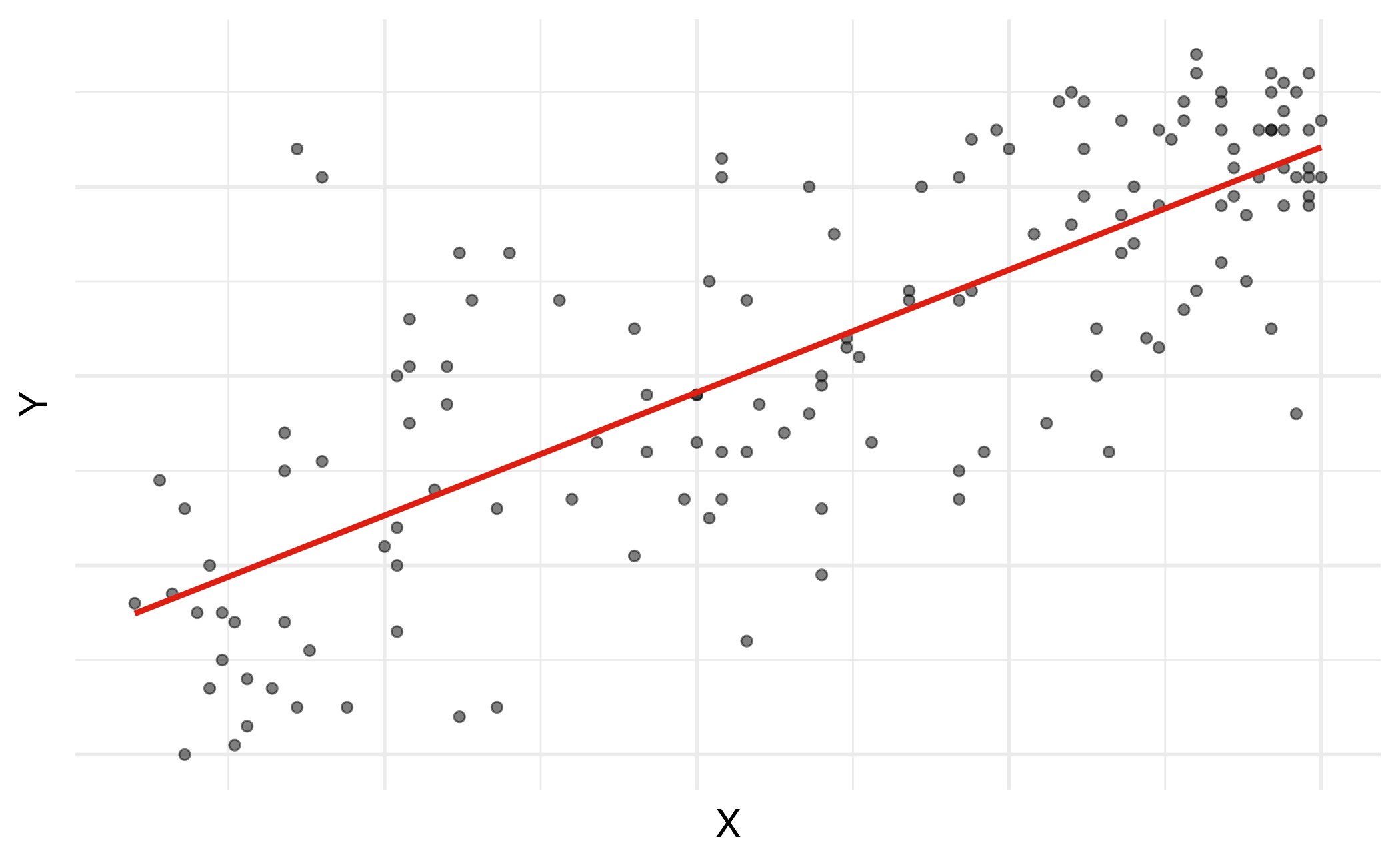
Models with a single predictor
Regression model
A regression model is a function that describes the relationship between the outcome, \(Y\), and the predictor, \(X\).
\[ \begin{aligned} Y &= \color{black}{\textbf{Model}} + \text{Error} \\ &= \color{black}{\mathbf{f(X)}} + \epsilon \end{aligned} \]
Regression model
\[ \begin{aligned} Y &= \color{#DF1E12}{\textbf{Model}} + \text{Error} \\ &= \color{#DF1E12}{\mathbf{f(X)}} + \epsilon \end{aligned} \]
Simple linear regression
Use simple linear regression to model the relationship between a quantitative outcome (\(Y\)) and a single quantitative predictor (\(X\)):
\[ \begin{aligned} Y &= f(X) \\ &= \beta_0 + \beta_1 X + \epsilon \end{aligned} \]
- \(\beta_1\): True slope of the relationship between \(X\) and \(Y\)
- \(\beta_0\): True intercept of the relationship between \(X\) and \(Y\)
- \(\epsilon\): Error (residual)
But we don’t know \(\beta_0\) and \(\beta_1\) - we only have a sample of 146 movies!
Simple linear regression
\[\Large{\hat{Y} = b_0 + b_1 X}\]
- \(b_1\): Estimated slope of the relationship between \(X\) and \(Y\)
- \(b_0\): Estimated intercept of the relationship between \(X\) and \(Y\)
- No error term!
- How do we choose values for \(b_1\) and \(b_0\)?
Choosing values for \(b_1\) and \(b_0\)
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| label: lm-values
#| viewerHeight: 700
#| viewerWidth: "100%"
#| standalone: true
library(shiny)
library(ggplot2)
library(fivethirtyeight)
library(bslib)
library(dplyr)
# Create movie_scores from fandango dataset
movie_scores <- fandango %>%
rename(
critics = rottentomatoes,
audience = rottentomatoes_user
)
# Calculate actual regression line parameters
actual_model <- lm(audience ~ critics, data = movie_scores)
actual_intercept <- coef(actual_model)[1]
actual_slope <- coef(actual_model)[2]
# Set default values slightly off from actual values
default_intercept <- round(actual_intercept + 10) # Add 10 to be "slightly wrong"
default_slope <- round(actual_slope - 0.2, 2) # Subtract 0.2 to be "slightly wrong"
ui <- page_sidebar(
# title = "Linear Regression: Movie Scores Explorer",
theme = bs_theme(
version = 5,
bootswatch = "default",
base_font_size = "22px" # Increased base font size
),
# Left sidebar with inputs
sidebar = sidebar(
width = "35%", # Increased width for more space
tags$style(HTML("
.irs-min, .irs-max, .irs-single, .irs-from, .irs-to, .irs-grid-text {
font-size: 20px !important;
}
.irs-grid-pol {
height: 6px !important;
}
.irs-bar, .irs-line {
height: 12px !important;
}
.irs-handle {
width: 24px !important;
height: 24px !important;
top: 26px !important;
}
.control-label {
font-size: 24px !important;
font-weight: bold !important;
margin-bottom: 10px !important;
}
")),
sliderInput(
"intercept",
"Intercept:",
min = 0,
max = 100,
value = default_intercept,
step = 1,
width = "100%"
),
tags$div(style = "margin-top: 30px;"), # Add spacing between sliders
sliderInput(
"slope",
"Slope:",
min = -2,
max = 2,
value = default_slope,
step = 0.05,
width = "100%"
)
),
# Main panel with plot
card(
full_screen = TRUE,
plotOutput("regressionPlot", height = "500px")
)
)
server <- function(input, output) {
# Create the plot
output$regressionPlot <- renderPlot({
# User defined regression line
user_intercept <- input$intercept
user_slope <- input$slope
# Create simple plot
ggplot(movie_scores, aes(x = critics, y = audience)) +
geom_point(alpha = 0.7, size = 3) + # Larger points
geom_abline(intercept = user_intercept, slope = user_slope,
color = "red", linewidth = 1.5) + # Thicker line
labs(
x = "Critics Score",
y = "Audience Score"
) +
theme_minimal(base_size = 16) + # Larger theme elements
theme(
axis.title = element_text(size = 18, face = "bold"),
axis.text = element_text(size = 16)
)
})
}
shinyApp(ui = ui, server = server)Residuals
\[\text{residual} = \text{observed} - \text{predicted} = y - \hat{y}\]
Least squares line
- The residual for the \(i^{th}\) observation is
\[e_i = \text{observed} - \text{predicted} = y_i - \hat{y}_i\]
- The sum of squared residuals is
\[e^2_1 + e^2_2 + \dots + e^2_n\]
- The least squares line is the one that minimizes the sum of squared residuals
Least squares line
Slope and intercept
Properties of least squares regression
The regression line goes through the center of mass point (the coordinates corresponding to average \(X\) and average \(Y\)): \(b_0 = \bar{Y} - b_1~\bar{X}\)
Slope has the same sign as the correlation coefficient: \(b_1 = r \frac{sd_Y}{sd_X}\)
Sum of the residuals is zero: \(\sum_{i = 1}^n \epsilon_i = 0\)
Residuals and \(X\) values are uncorrelated
Interpreting the slope
The slope of the model for predicting audience score from critics score is 0.519. Which of the following is the best interpretation of this value?
- For every one point increase in the critics score, the audience score goes up by 0.519 points, on average.
- For every one point increase in the critics score, we expect the audience score to be higher by 0.519 points, on average.
- For every one point increase in the critics score, the audience score goes up by 0.519 points.
- For every one point increase in the audience score, the critics score goes up by 0.519 points, on average.
Interpreting slope & intercept
\[\widehat{\text{audience}} = 32.3 + 0.519 \times \text{critics}\]
- Slope: For every one point increase in the critics score, we expect the audience score to be higher by 0.519 points, on average.
- Intercept: If the critics score is 0 points, we expect the audience score to be 32.3 points.
Is the intercept meaningful?
✅ The intercept is meaningful in context of the data if
- the predictor can feasibly take values equal to or near zero or
- the predictor has values near zero in the observed data
🛑 Otherwise, it might not be meaningful!
Statistical inference with a single predictor
Birth weights and gestation time
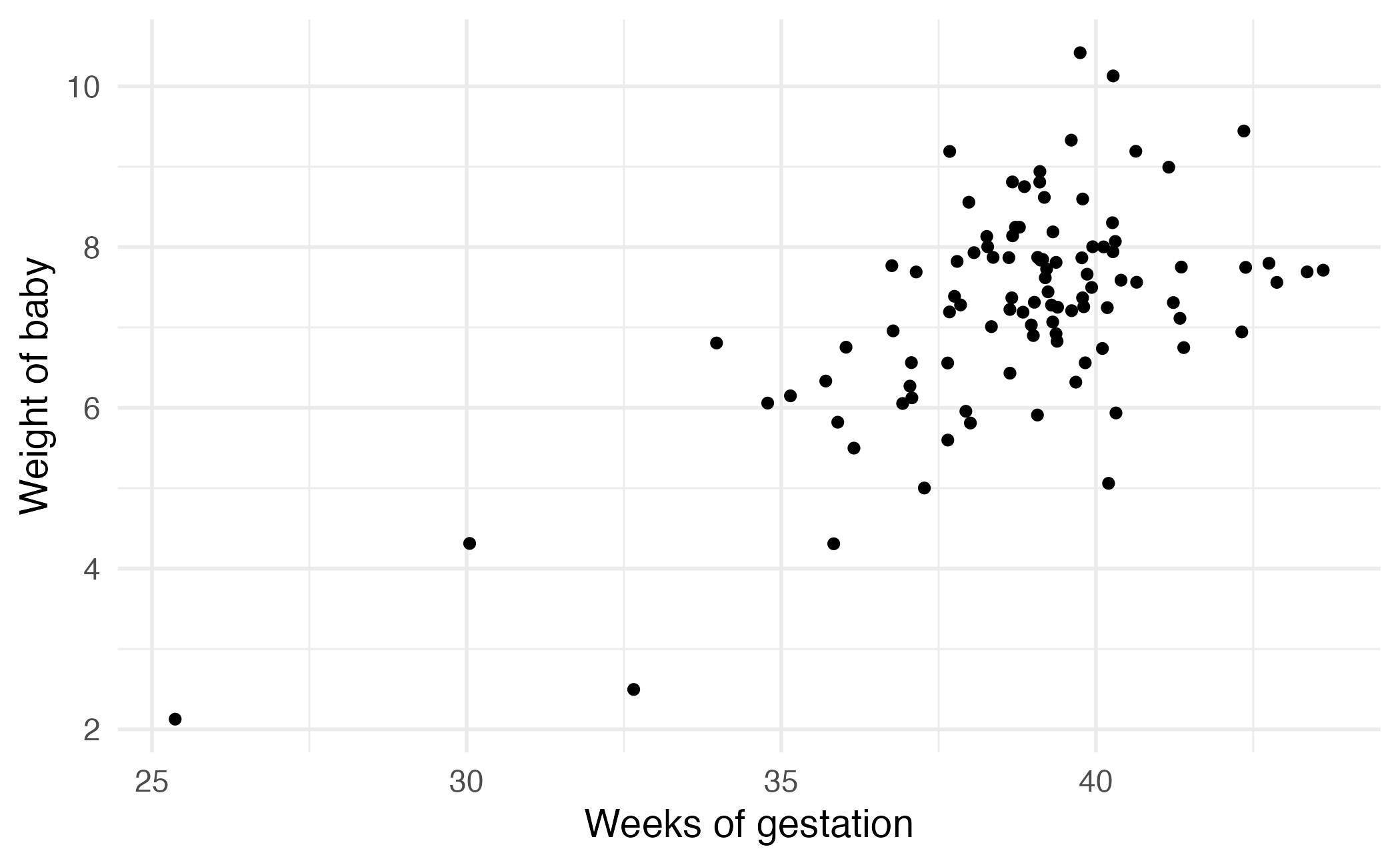
Image credit: IMS
Null hypothesis framework
Population of interest: All births in the United States
- \(H_0: \beta_1= 0\), there is no linear relationship between
weightandweeks. - \(H_A: \beta_1 \ne 0\), there is some linear relationship between
weightandweeks.
Permutation-based approach
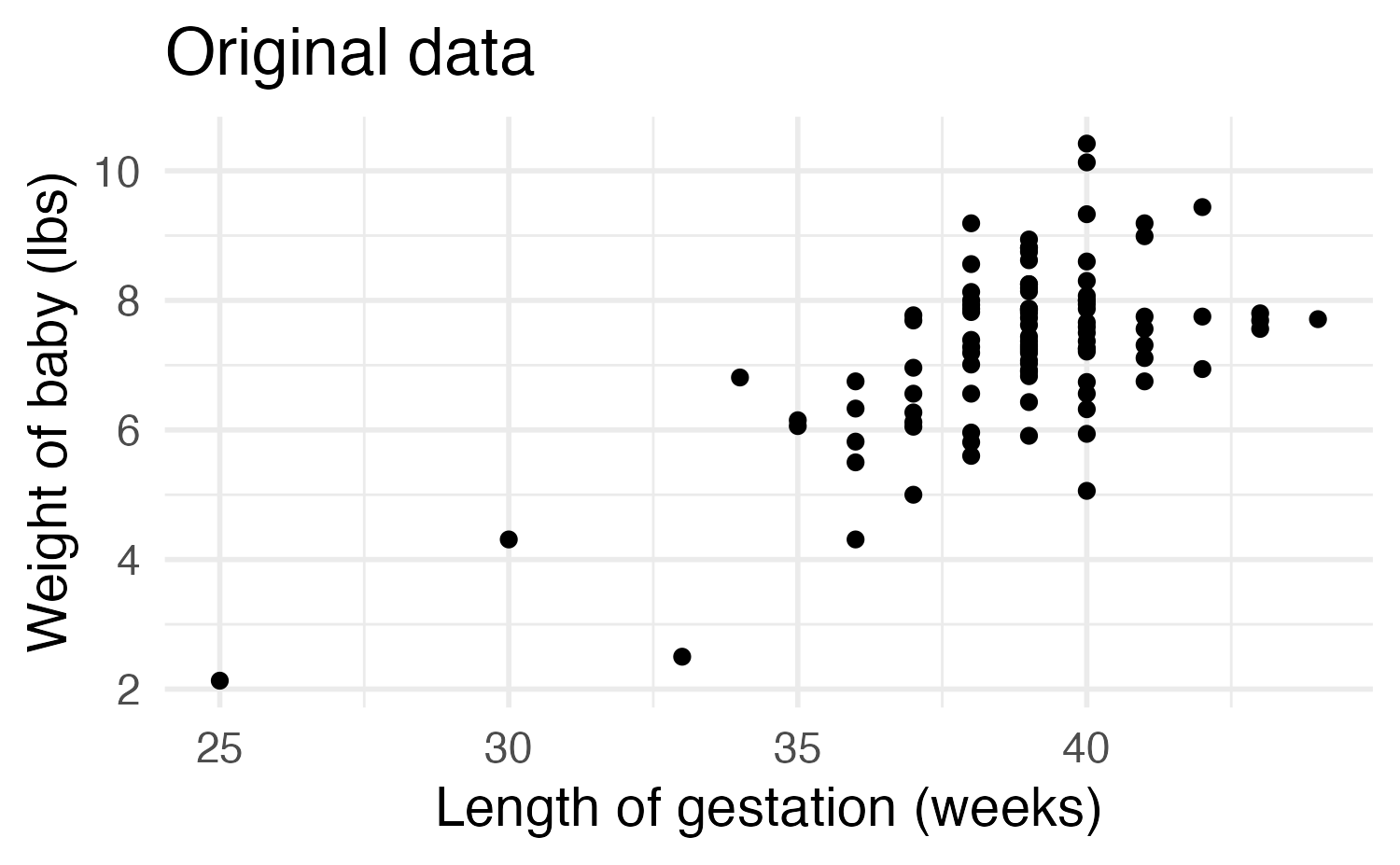
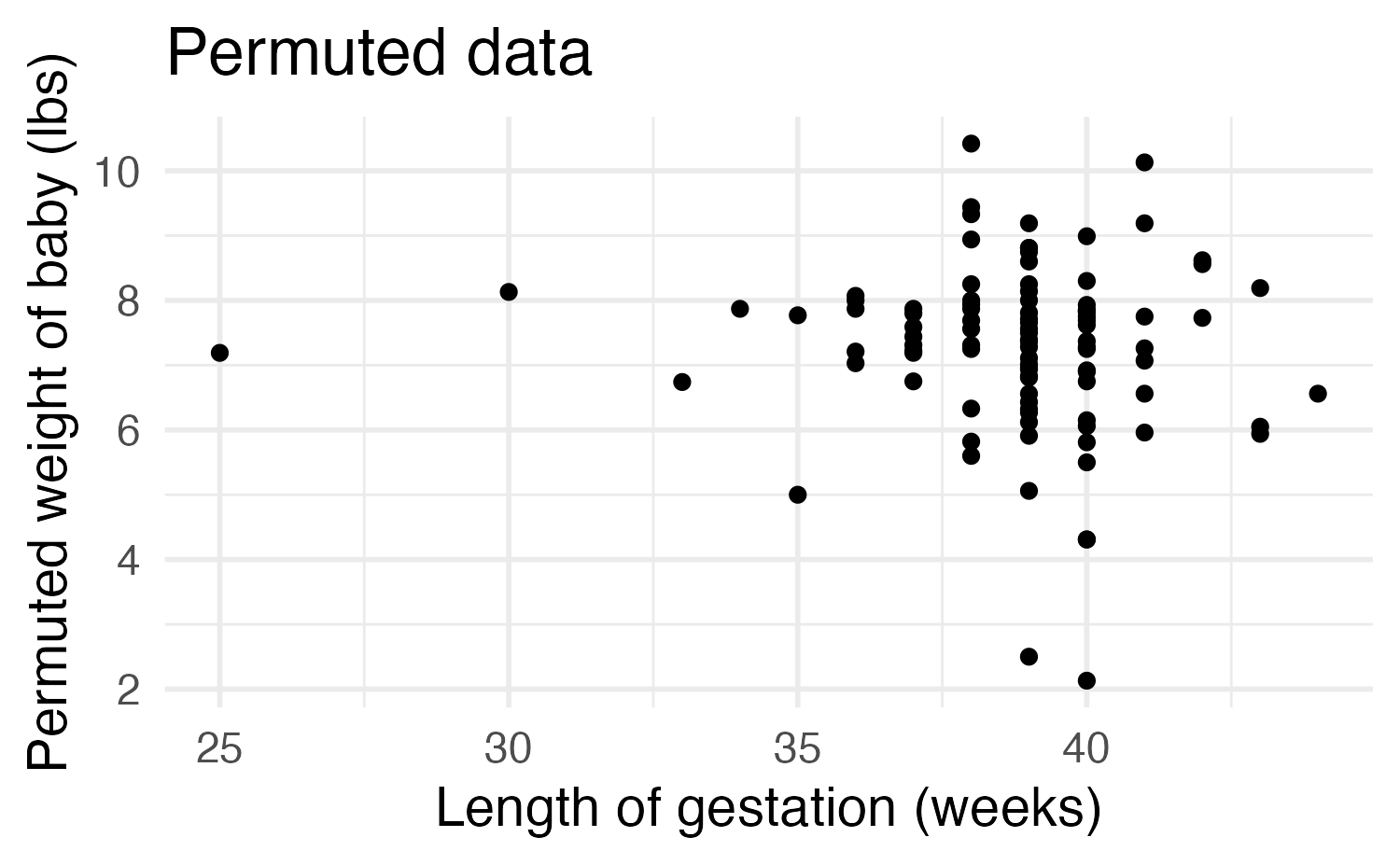
Image credit: IMS
Observed data
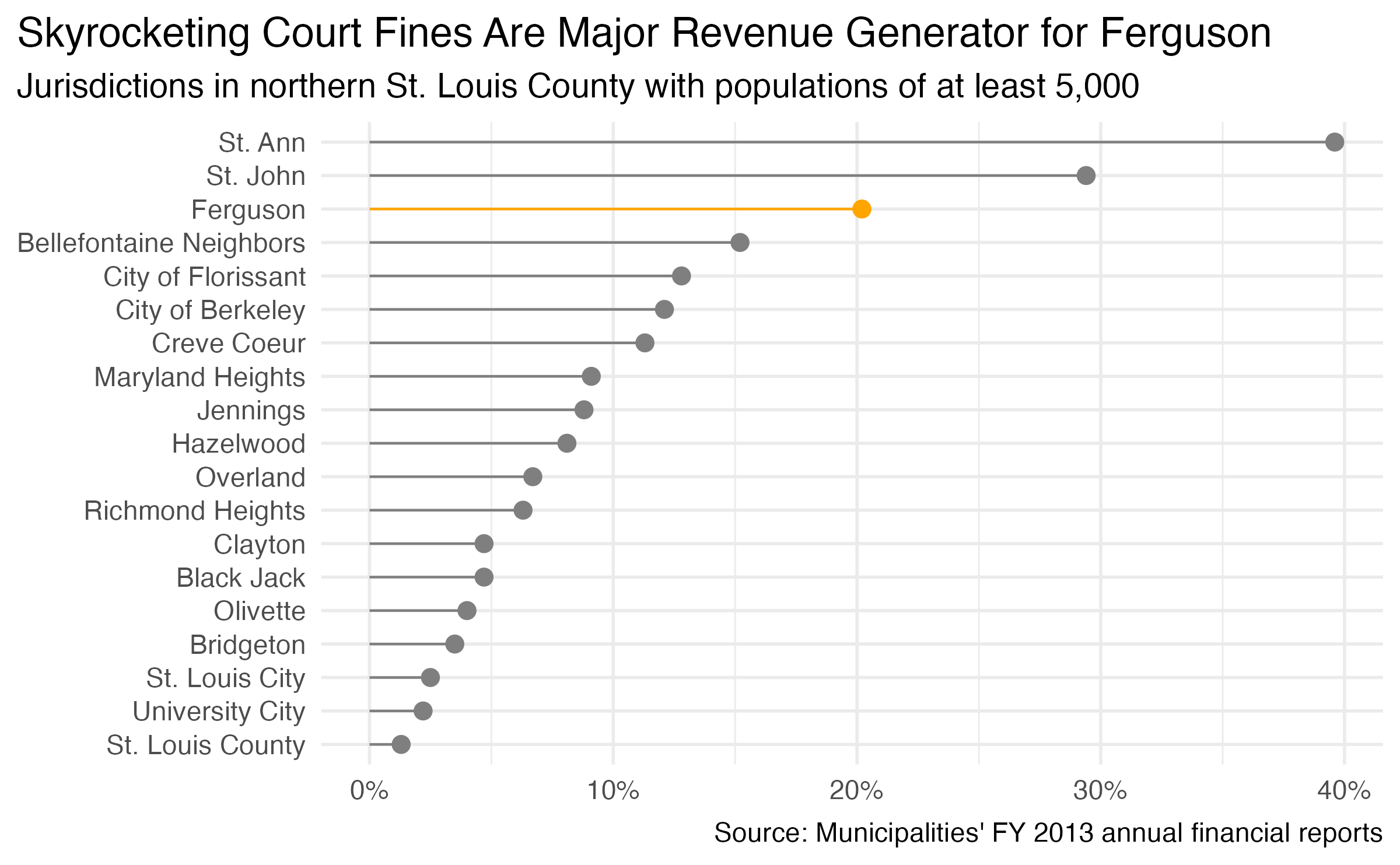
| Characteristic | Beta | SE | Statistic | 95% CI | p-value |
|---|---|---|---|---|---|
| (Intercept) | -5.7 | 1.61 | -3.54 | -8.9, -2.5 | <0.001 |
| weeks | 0.34 | 0.042 | 8.07 | 0.25, 0.42 | <0.001 |
| Abbreviations: CI = Confidence Interval, SE = Standard Error | |||||
Variability of the statistic
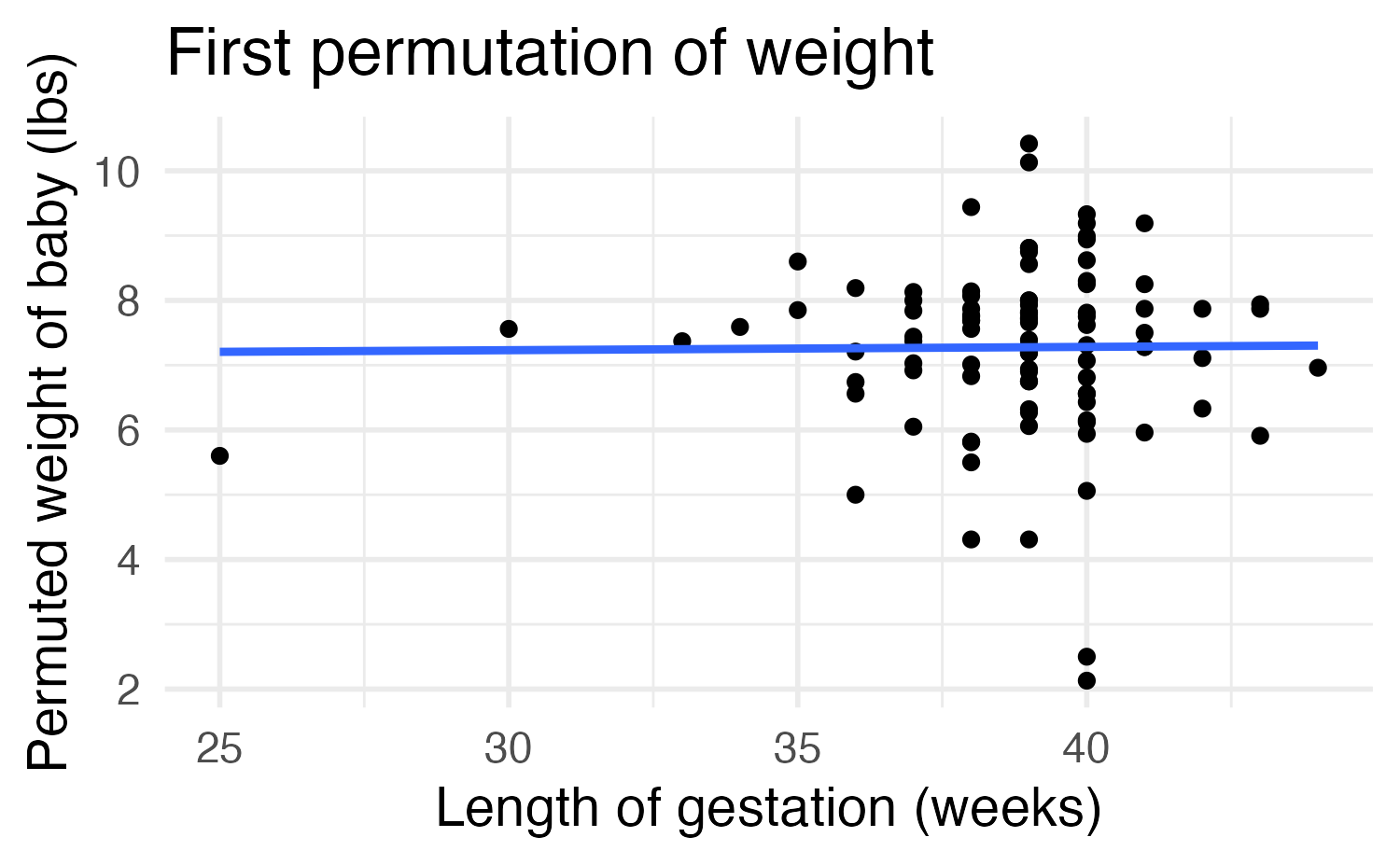
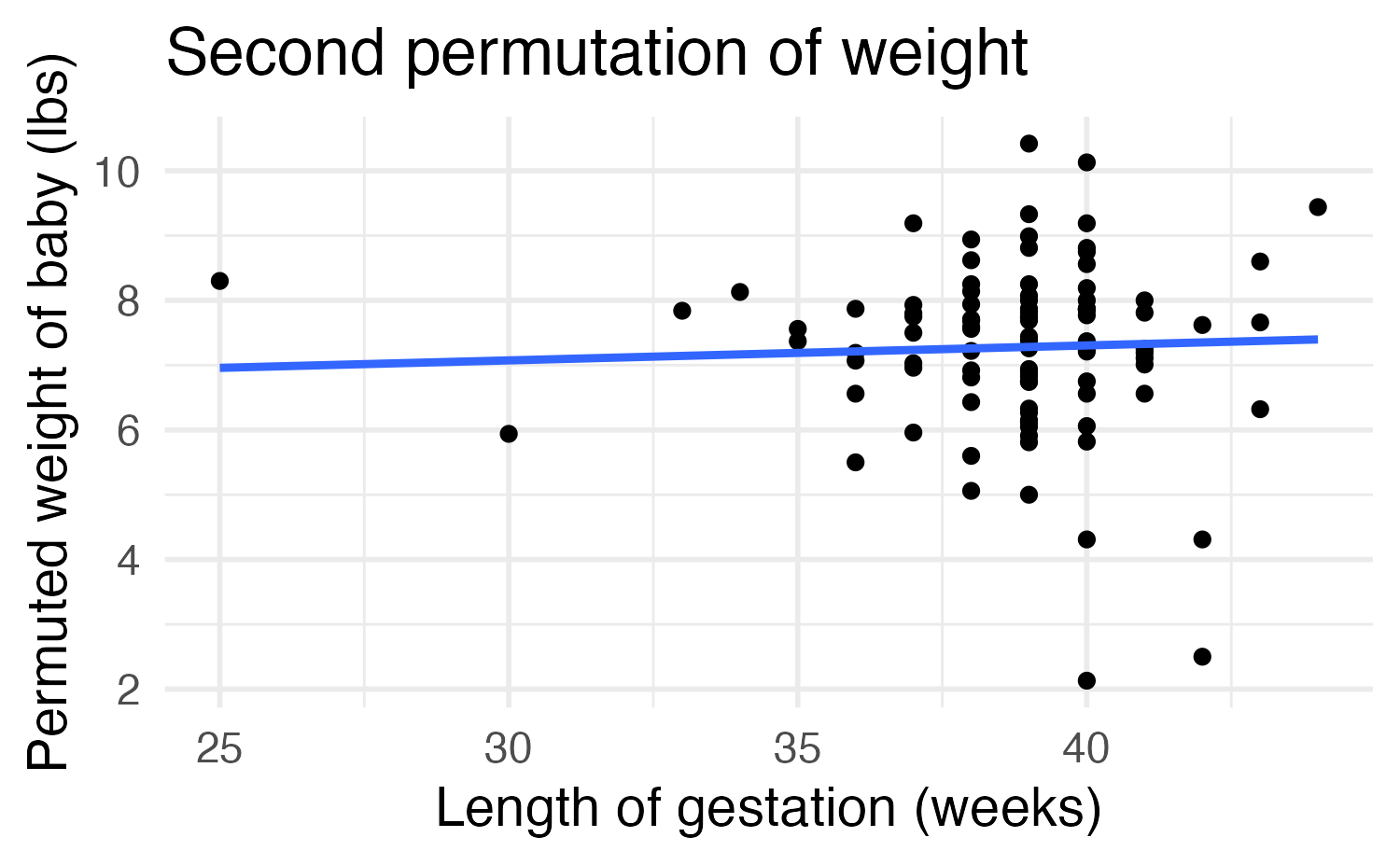
Image credit: IMS
Observed statistic vs. null statistics
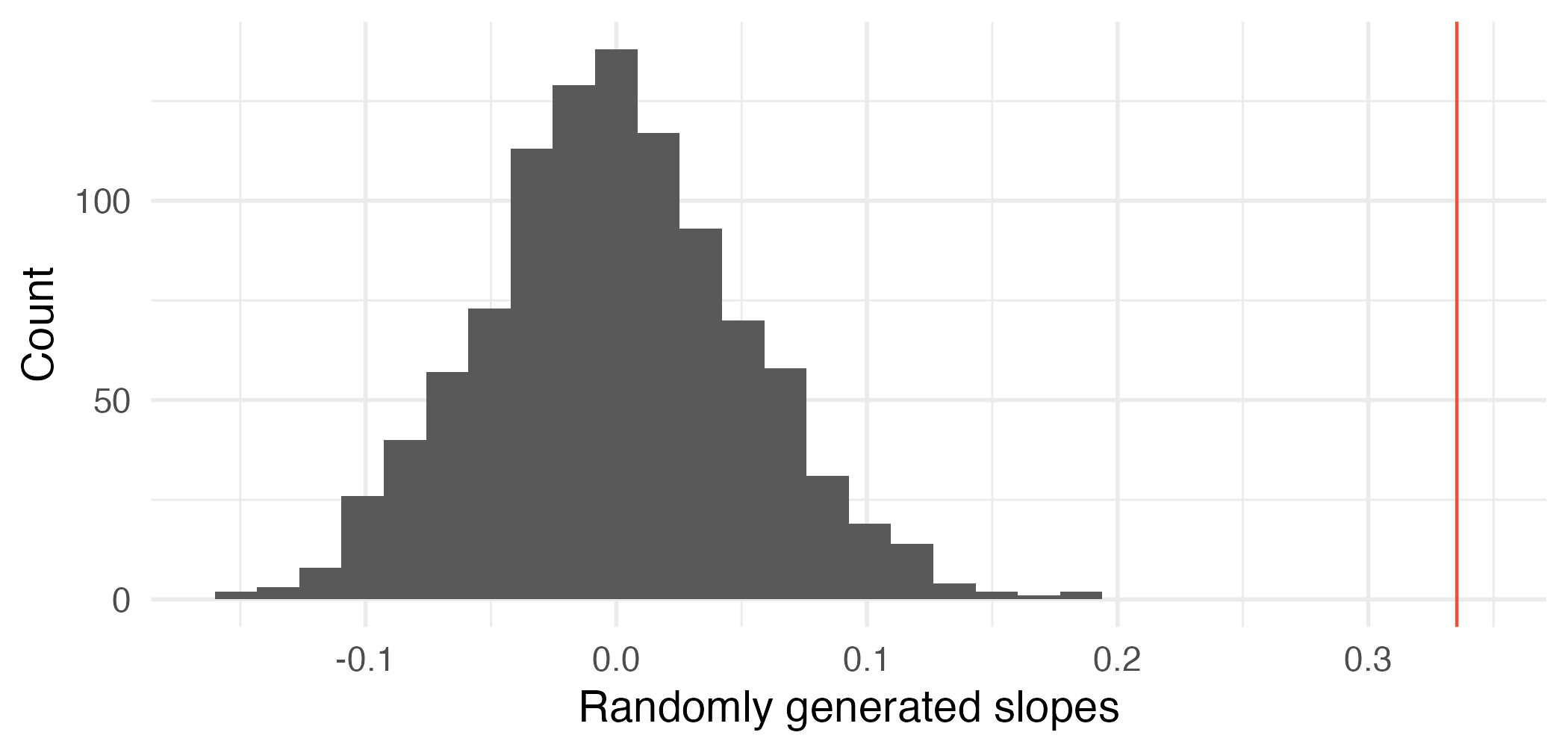
Image credit: IMS
Bootstrap CI for the slope
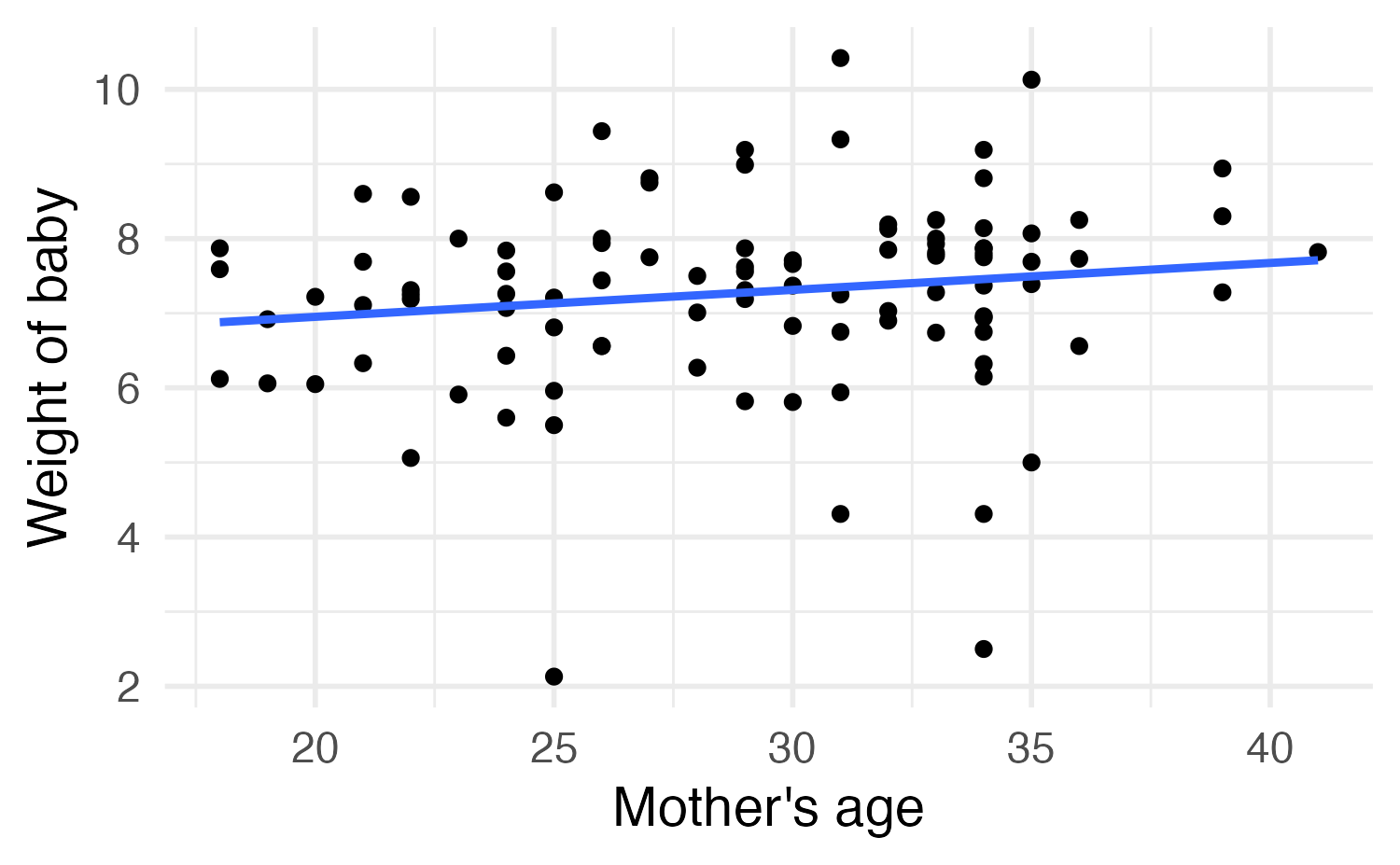
| Characteristic | Beta | SE | Statistic | 95% CI | p-value |
|---|---|---|---|---|---|
| (Intercept) | 6.2 | 0.708 | 8.79 | 4.8, 7.6 | <0.001 |
| mage | 0.04 | 0.024 | 1.50 | -0.01, 0.08 | 0.14 |
| Abbreviations: CI = Confidence Interval, SE = Standard Error | |||||
Image credit: IMS
Bootstrap resampling
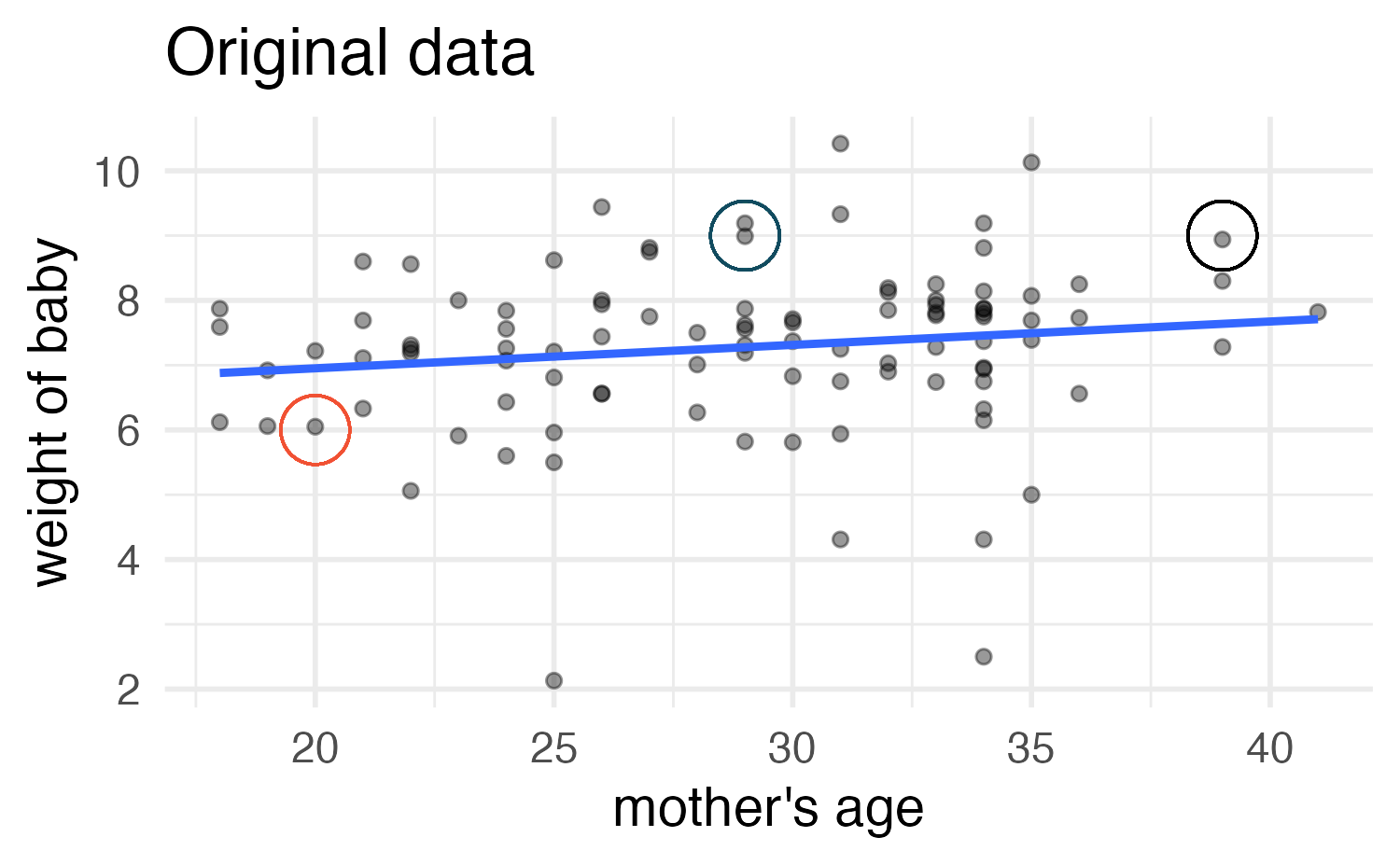
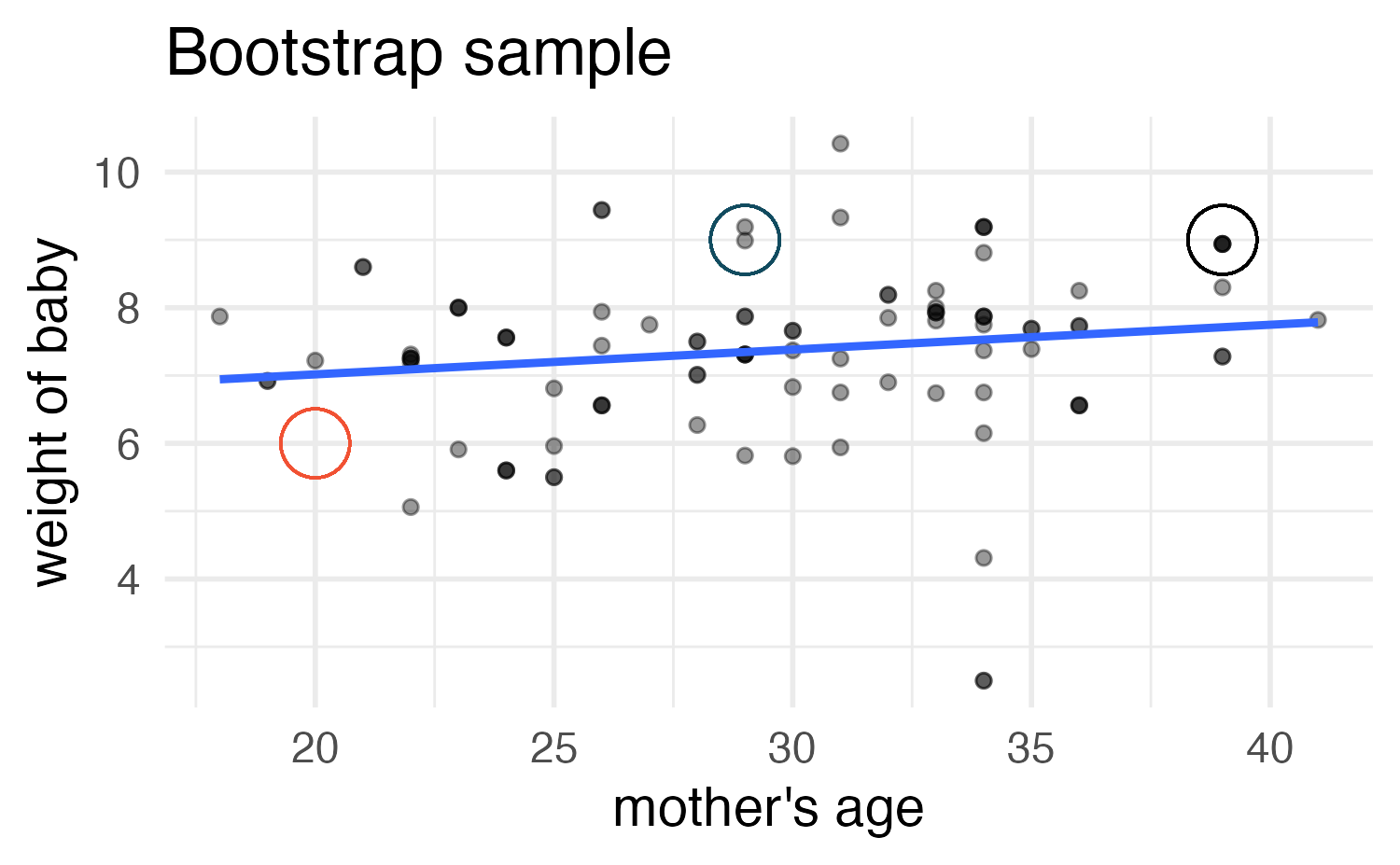
Image credit: IMS
Bootstrap resampling (repeated)
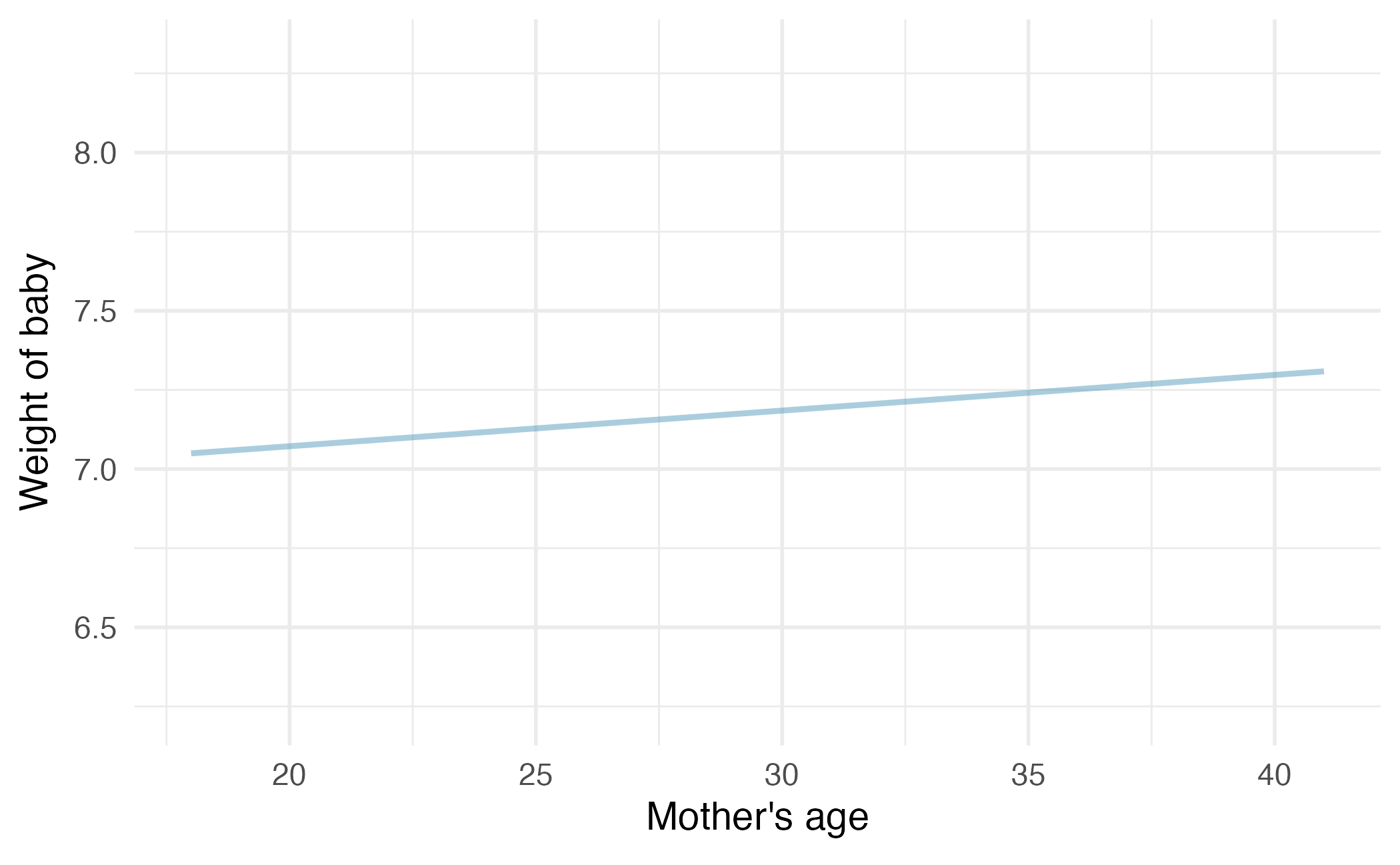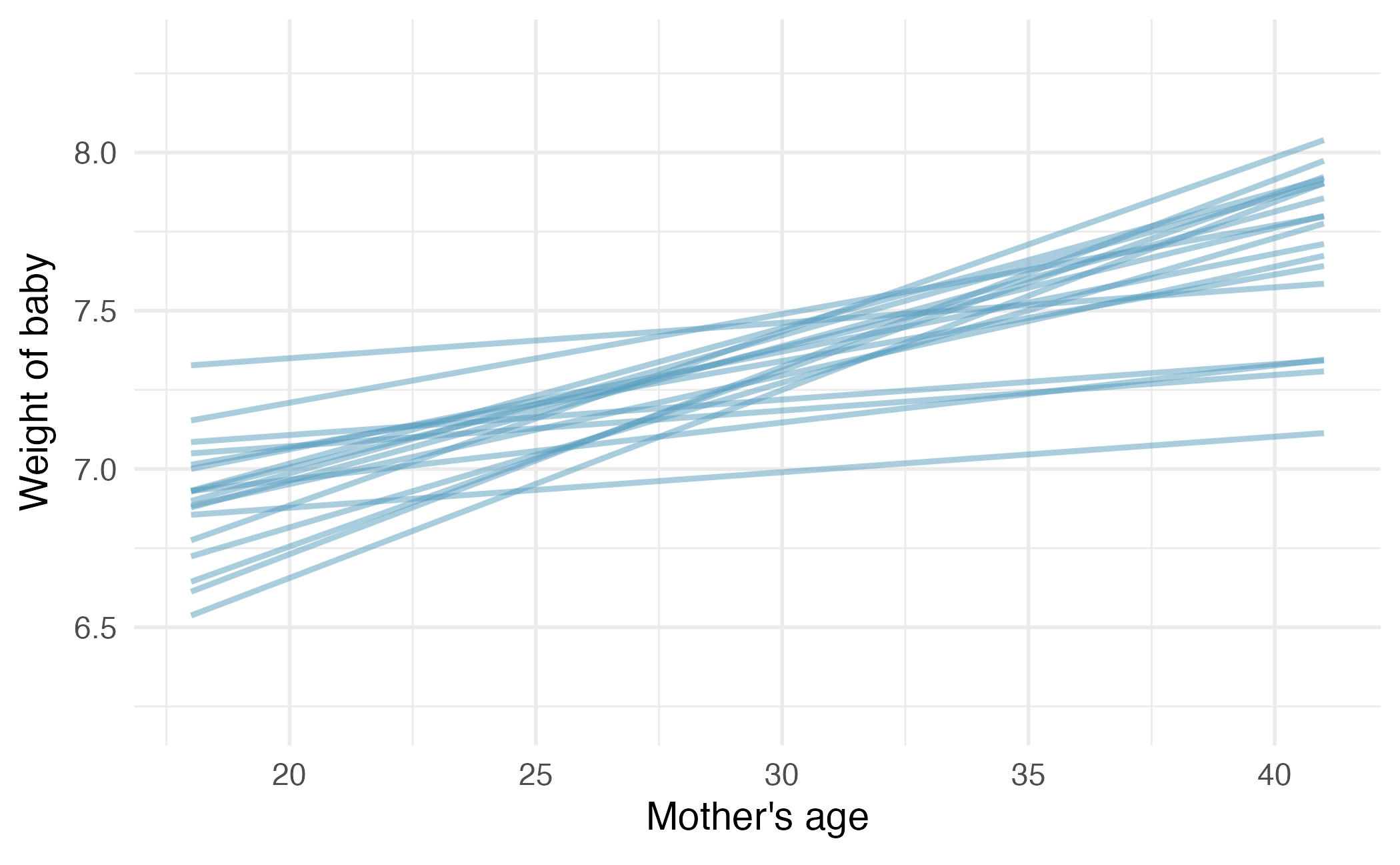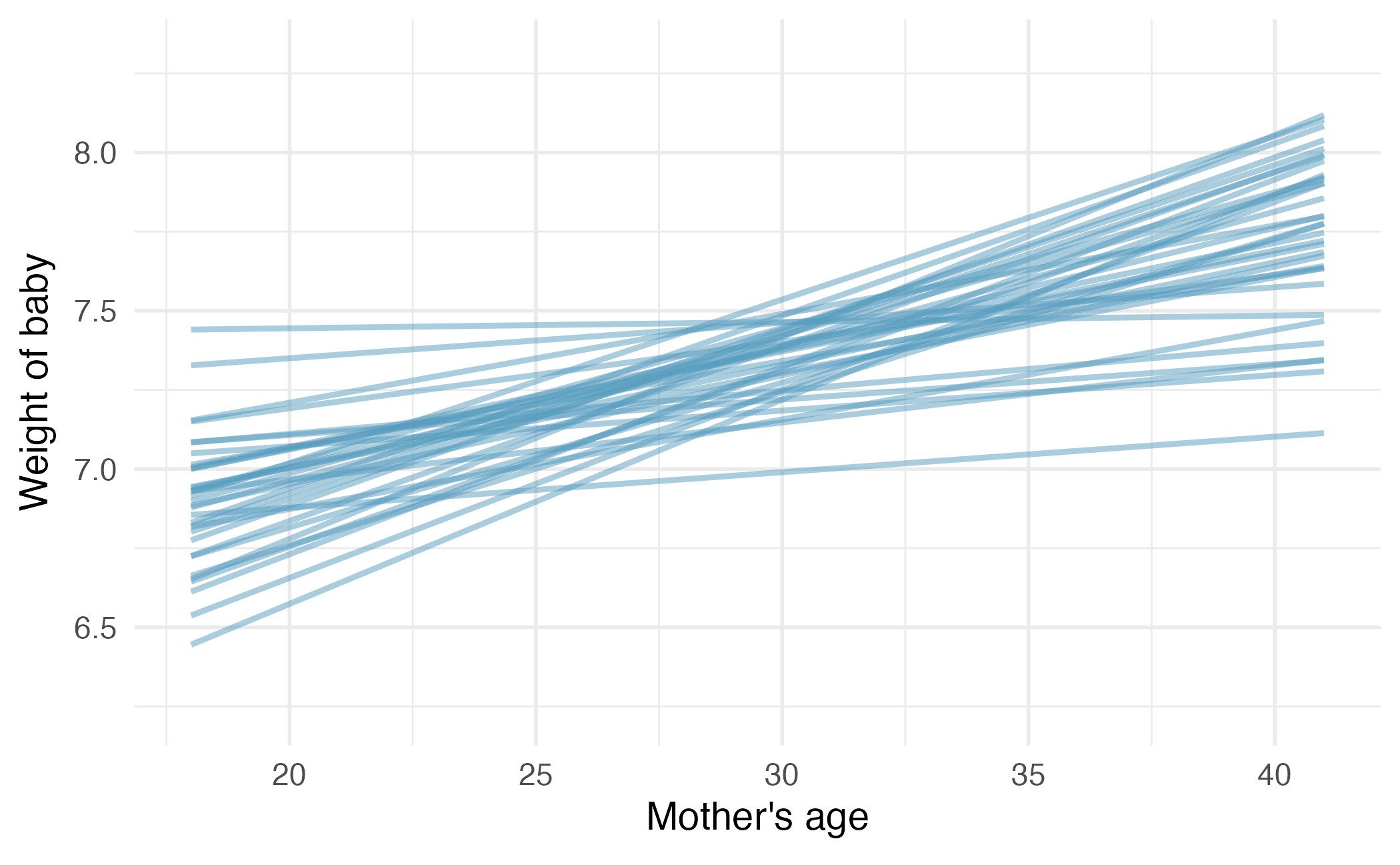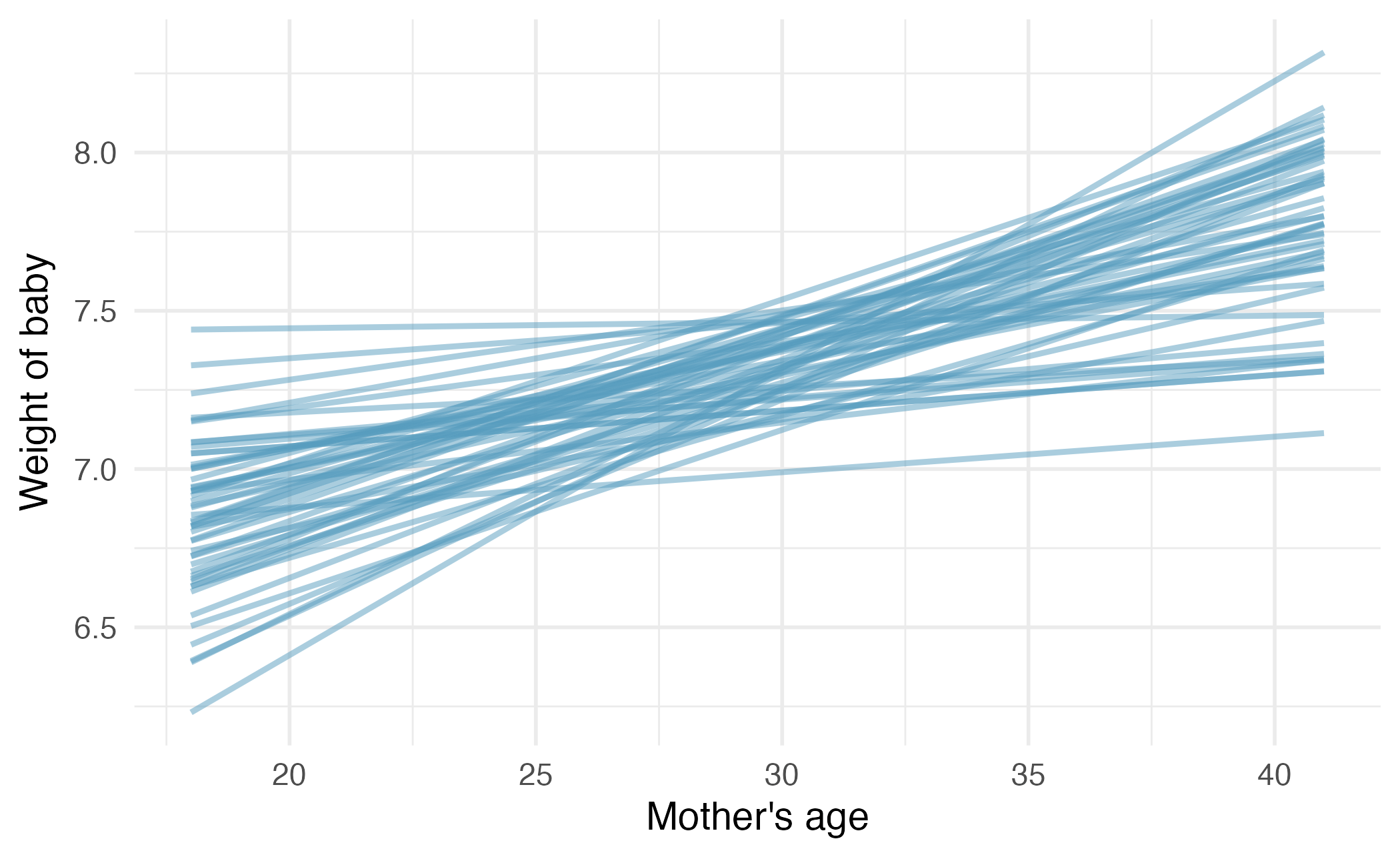
Image credit: IMS
Bootstrap CI for the slope
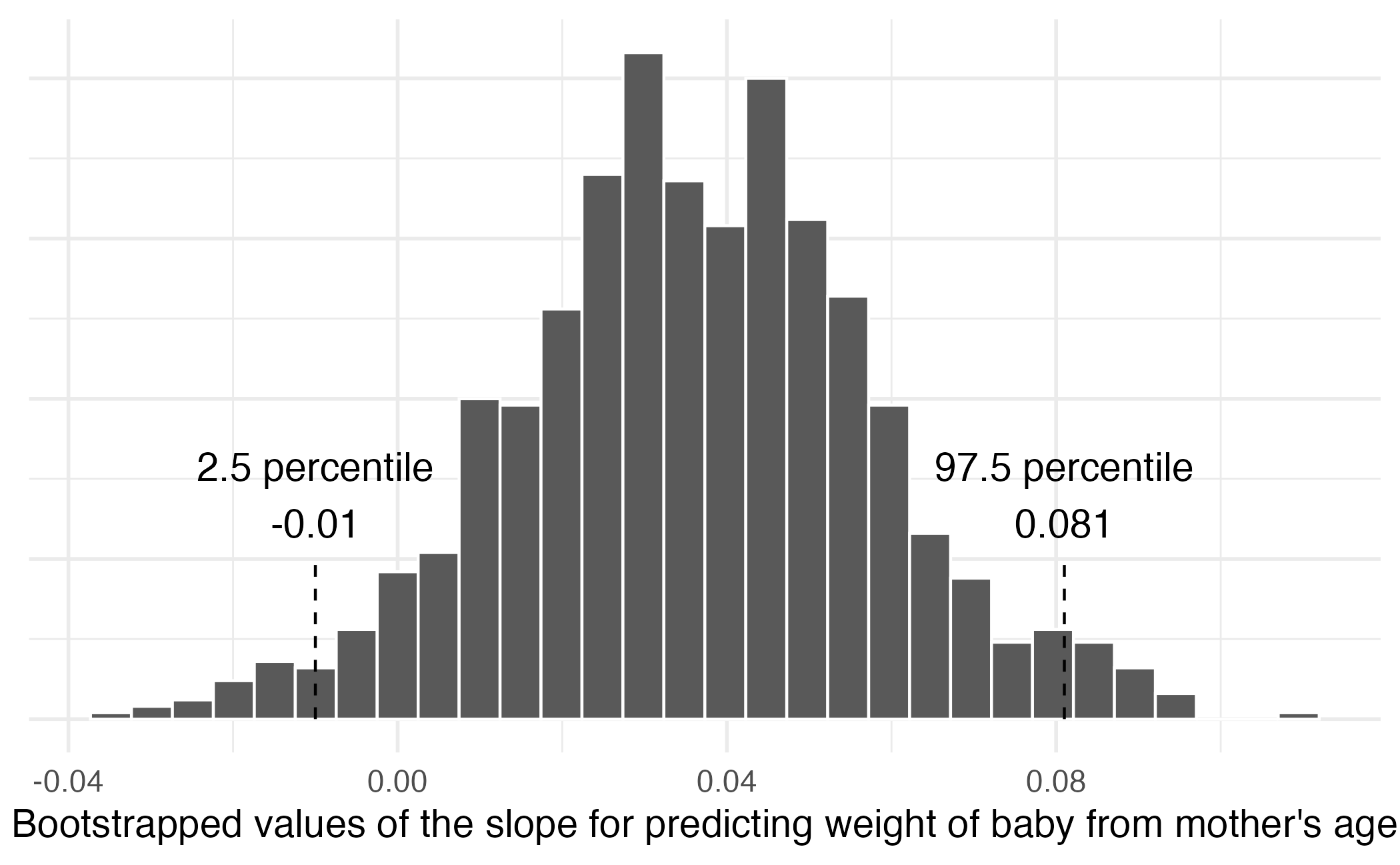
Image credit: IMS
Checking model conditions
- Linearity
- Independent observations
- Nearly normal residuals
- Constant or equal variability
Violations of model conditions
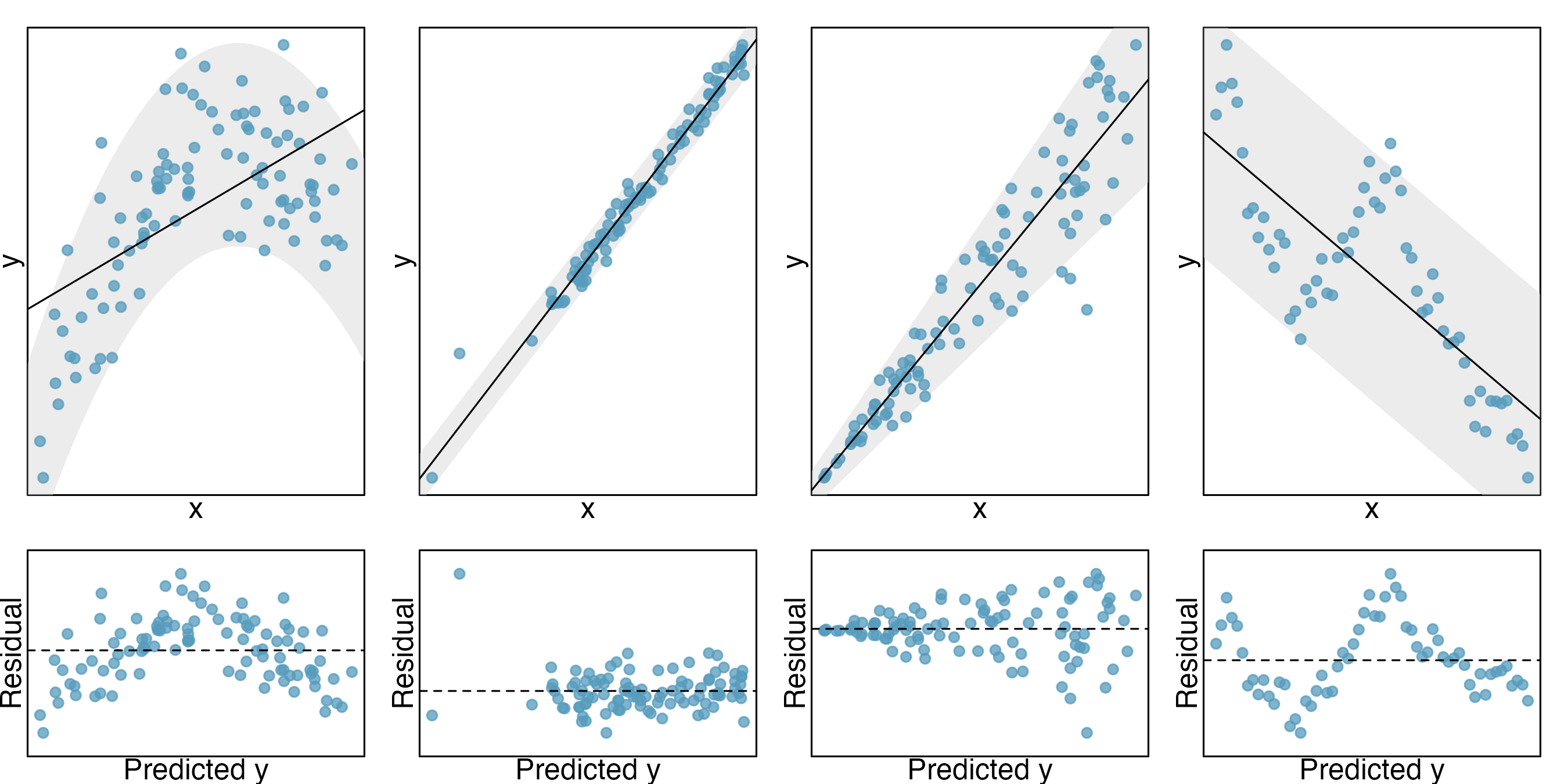
Image credit: IMS
Application exercise
ae-16
Instructions
- Go to the course GitHub org and find your
ae-16(repo name will be suffixed with your GitHub name). - Clone the repo in RStudio, run
renv::restore()to install the required packages, open the Quarto document in the repo, and follow along and complete the exercises. - Render, commit, and push your edits by the AE deadline – end of the day
Wrap up
Recap
- Linear regression fits a line to the relationship between \(X\) and \(Y\)
- It estimates coefficients that minimize the sum of squared error (residuals)
- We can use permutation tests and bootstrapping to make inferences about the coefficients
- Linear regression has specific assumptions that must be met in order to make valid inferences
Acknowledgments
- Draws upon material from Data Science in a Box licensed under Creative Commons Attribution-ShareAlike 4.0 International